§. ĐỊNH LÍ TA-LÉT TRONG TAM GIÁC

A/ KIẾN THỨC VÀ KĨ NĂNG CẦN NHỚ

I. Tỉ số của hai đoạn thẳng

Định nghĩa : Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.

II. Đoạn thẳng tỉ lệ

Định nghĩa : Hai đoạn thẳng AB và CD gọi là tỉ lệ với hai đoạn thẳng A'B' và C'D' nếu có tỉ lệ thức :

III. Định lí Ta-lét trong tam giác

Nếu một đường thẳng song song

với một cạnh của tam giác và cắt

hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.

IV. Định lí Ta-lét đảo

Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.

Cho tam giác ABC (h.4)

 Þ a // BC

II. Hệ quả của định lí Ta-lét

Nếu một đường thẳng cắt hai cạnh (hoặc cắt phần kéo dài của hai cạnh) của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.

Cho tam giác ABC : a // BC Þ . (h.5)

B/ BÀI TẬP

1. Cho góc xAy khác góc bẹt. Trên tia Ax lấy các điểm B, C. Qua B và C vẽ hai đường thẳng song song cắt Ay lần lượt ở D và E. Qua E vẽ đường thẳng song song với CD cắt tia Ax ở F.

a) So sánh  và  ;

b) Chứng minh rằng: AC² = AB.AF

2. Cho G là trọng tâm tam giác ABC. Qua G vẽ đường thẳng song song với AB cắt BC tại D. Chứng minh rằng : BD = .

3. Đường thẳng d cắt các cạnh AB, AD và đường chéo AC của hình bình hành ABCD lần lượt tại E, F và O.

Chứng minh rằng .

4. Cho tam giác ABC có AM là đường trung tuyến. N là điểm trên đoạn thẳng AM. Gọi D là giao điểm của CN và AB, E là giao điểm của BN và AC.  Chứng minh rằng .

5. Cho hình bình hành ABCD tâm O. Gọi M, N lần lượt là trung điểm của BO, AO. Lấy điểm F trên cạnh AB sao cho tia FM cắt cạnh BC tại E và tia FN cắt cạnh AD tại K. Chứng minh rằng:

a)                   b) BE + AK ³ BC.

6. Cho tam giác vuông cân ABC có góc C = 90⁰ .Từ C kẻ một tia vuông góc với trung tuyến AM cắt AB ở D. Hãy tính tỉ số  .  

7. Cho điểm E thuộc cạnh AC của DABC . Qua B kẻ một đường thẳng I.Đường thẳng qua E và song song với BC cắt I tại N. Đường thẳng qua E và song song với AB cắt I tại M. Chứng minh rằng AN // CM.

8. Cho hình thang ABCD có BC // AD. Trên AC kéo dài lấy 1 điểm P tùy ý . Đường thẳng qua P và trung điểm của BC cắt AB tại M và đường thẳng qua P và trung điểm của AD cắt CD tại N. Chứng minh rằng MN // AD.

9. Tứ giác ABCD có M, N lần lượt là trung điểm của các đường chéo AC và BD. Gọi G là trọng tâm D ABC. Nối GC cắt MN tại O . Chứng minh rằng : OC = 3 OG

10. Cho hình thang ABCD ( AB // CD ) với AB = a ; CD = b. Gọi I là giao điểm của hai đường chéo . Đường thẳng qua I và song song với AB cắt hai cạnh bên tại E và F. Chứng minh rằng :

11. Hình bình hành ABCD. Gọi M là một điểm trên đường chéo AC. Vẽ ME vuông góc với AB và MF vuông góc với AD. Chứng minh rằng :

12. Hình thang ABCD đáy lớn CD. Qua A vẽ đường thẳng AK // BC cắt BD tại E. Qua B vẽ đường thẳng BI // AD cắt AC tại F ( K ; I thuộc CD). Chứng minh rằng:

a)      EF // AB

b)      AB² = CD . EF.

13. Cho 1 điểm M nằm trong D ABC. Đường thẳng  qua M và trọng tâm G của tam giác cắt BC; CA và AB theo thứ tự D, E, F. Chứng minh rằng

14. Cho D ABC cân tại A. Hai điểm D và E theo thứ tự thay đổi trên AB và BC. Kẻ DF vuông góc với BC. Chứng minh rằng nếu  thì đường thẳng qua E và vuông góc với DE luôn đi qua I điểm cố định.

15. Cho tam giác ABC, trọng tâm G, đường thẳng ( d) qua G cắt các cạnh AB và AC tại M và N. Chứng minh rằng : AM. AN = AM. NC + AN . MB.

16. Cho tam giác ABC vuông tại A. Giả sử đường cao AH, trung tuyến BM, và phân giác trong CN đồng quy. Chứng minh rằng BH = AC.

17. Cho tam giác ABC, AM, BN và CP cắt nhau tại I. Tìm I để:  nhỏ nhất.

18.  Cho tứ giác ABCD. Đường thẳng qua A song song với BC cắt BD tại P và đường thẳng qua B song song với AD cắt AC ở Q.

Chứng minh rằng PQ // CD.

19.  Lấy một điểm O trong tam giác ABC, các tia AO, BO, CO cắt BC, AC, AB lần lượt tại P, Q, R.

Chứng minh rằng .

20. Cho A¢, B¢, C¢ lần lượt nằm trên cạnh BC, AC, AB của tam giác ABC. Biết rằng AA¢, BB¢, CC¢ đồng quy tại M. Chứng minh rằng :

.

21. Cho một điểm M ở trong góc xOy. Một đường thẳng d qua M cắt 2 cạnh của góc ở A và B . Chứng minh rằng tổng  không phụ thuộc vị trí của d.

22. Cho hình bình hành ABCD . Một đường thẳng bất kỳ qua A cắt BD, CD và BC lần lượt tại E, F và G.

Chứng minh rằng :.

23. Cho tam giác ABC và trung tuyến AD. Một đường thẳng bất kỳ song song với AD cắt BC, CA, AB lần lượt tại E, N, M .

Chứng minh rằng:

24. DABC ( AB < AC ) có trung tuyến AM; phân giác AD. Đường thẳng qua M và song song với AD cắt AB tại E và AC tại F . Chứng minh :

a) DAEF cân

b) AC – AB = 2 AE.

§.TÍNH CHẤT ĐƯỜNG PHÂN GIÁC CỦA TAM GIÁC

A/ KIẾN THỨC VÀ KĨ NĂNG CẦN NHỚ

I. Định lí :

Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.

AD là phân giác góc BAC

Þ  

II. Chú ý

Định lí vẫn đúng với tia phân giác của góc ngoài của tam giác.

AE¢ là tia phân giác góc BAx (AB ¹ AC)

Þ  (h.9)

B/ BÀI TẬP

1.  Cho  ABC, AD là đường phân giác. Chứng minh : .

2. Tam giác ABC vuông tại A có AB = 8 cm, BC = 10 cm và có AD là đường phân giác. Tính các đoạn DB, DC.

3. Cho tam giác ABC và AD, BE, CF là ba đường phân giác. Chứng minh rằng  = 1.

4. Cho tam giác ABC, AM là đường trung tuyến. Các đường phân giác của góc BMA và góc CMA cắt AB và AC tương ứng tại D và E. Chứng minh rằng DE // BC.

5. Cho tam giác ABC. O là giao điểm các đường phân giác ta đặt AB = c, AC = b, BC = a. AO cắt BC tại D. Tính DB,  theo a, b, c.

6. Cho tam giác ABC cân tại A, (AB = AC = m, BC = n),  = 36⁰.

Chứng minh rằng n² + m.n – m² = 0

7. Chứng minh rằng tam giác ABC là tam giác vuông nếu các đường phân giác BD, CE cắt nhau tại I thoả mãn: .

8. Cho 3 tia Ox, Oy, Oz tạo thành chứng minh rằng nếu A, B, C là 3 điểm thẳng hàng trên Ox, Oy, Oz thì ta có                            9. Gọi d_a , d_b , d_c là độ dài các đường phân giác thuộc các cạnh a, b, c của tam giác ABC.Chứng minh

10. Gọi b và c là độ dài các cạnh AC,AB của tam giác ABC,d_a là độ dài phân giác thuộc cạnh BC. Chứng minh rằng điều kiện cần và đủ để tam giác ABC có  là

11. Cho ABC trung tuyến BM cắt phn gic CD của  tại P. Chứng minh :

12. Cho ABC vuơng tại A(AB < AC), kẻ đường cao AH, trung tuyến AM. Đường thẳng vuơng gĩc với AM tại A cắt đường thẳng BC tại D. Chứng minh rằng :  a) AB l tia phngic gĩc DAH

                                    b) BH. CD = BD. CH

13. Cho ABC, các tia phân giác trong BM, CN (MAC, NAB) cắt nhautại D. Chứng minh rằng :

            ABC vuơng tại A2BD. CD = BM. CN

14. Cho ABC, có AD, BE, CF theo thứ tự là các đường phân giác trong của góc A, B, C. Gọi I và K theo thứ tự là các điểm đối xứng với A qua các đường thẳng BE, CF, G và H theo thứ tự là các điểm đối xứng với B và C qua đường thẳng AD. Chứng minh rằng: GI//HK.

§. KHÁI NIỆM HAI TAM GIÁC ĐỒNG DẠNG. TRƯỜNG HỢP ĐỒNG DẠNG THỨ NHẤT

I. KHÁI NIỆM HAI TAM GIÁC ĐỒNG DẠNG

1. Tam giác đồng dạng

a) Định nghĩa

Tam giác A'B'C' gọi là đồng dạng với tam giác ABC nếu:

; ; ;  =  =

Tam giác A'B'C' đồng dạng với tam giác ABC được kí hiệu là
DA'B'C' ∽ DABC (viết theo thứ tự cặp đỉnh tương ứng).

Tỉ số các cạnh tương ứng  =  = = k gọi là tỉ số đồng dạng.

b) Tính chất

Tính chất 1. Mỗi tam giác đồng dạng với chính nó

Tính chất 2. Nếu DA'B'C' ∽ DABC thì DABC ∽ DA'B'C'

Tính chất 3. Nếu DA'B'C' ∽ DA''B''C" và DA''B''C" ∽ DABC thì
D A'B'C' ∽ DABC.

2. Định lí

Nếu một đường thẳng cắt hai cạnh của

tam giác và song song với cạnh còn lại

thì nó tạo thành một tam giác mới đồng

dạng với tam giác đã cho.

Cho DABC.

MN // BC Þ DAMN ∽ DABC (h.12)

Chú ý

Định lí cũng đúng cho trường hợp đường thẳng a cắt phần kéo dài hai cạnh của tam giác và song với cạnh còn lại.

II. TRƯỜNG HỢP ĐỒNG DẠNG THỨ NHẤT

Định lí : Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.

DABC và DA¢B¢C¢ có  

Þ DABC ∽ DA¢B¢C¢ (c.c.c)

BÀI TẬP

1. Cho DABC ∽ DA¢B¢C¢. Chứng tỏ rằng 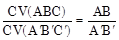 (với CV là chu vi tam giác).

2. Cho tam giác ABC, vẽ tam giác A¢B¢C¢ đồng dạng với tam giác ABC theo tỉ số đồng dạng k = .

3. Cho hai tam giác MNP và RSK có MN = 9 cm, MP = 12 cm,
NP = 15cm, RS = 5cm, KR = 3cm, KS = 4cm. Chứng minh rằng  

4. Cho hai tam giác ABC và DEF có : AB = 48cm, AC = 20cm,
BC = 52cm, DE = 6cm, DF = 2,5cm, AC = 5cm, BC = 13cm,
 = 90⁰. Chứng minh rằng

5. Cho hình thang ABCD (AB // CD), O là giao điểm của AC và BD. Chứng minh rằng DOAB ∽ DOCD.

6. a) Cho tam giác ABC. Các điểm D, E, F lần lượt là trung điểm các cạnh AB, BC, AC. Chứng minh rằng DEFD ∽ DABC

b) Cho M là điểm tuỳ ý trong tam giác ABC. Gọi A¢, B¢, C¢ lần lượt là trọng tâm của các tam giác MBC, MCA, MAB. Chứng minh rằng DABC ∽ DA¢B¢C¢.

7. Cho tam giác nhọn ABC. Các đường cao AD và BE cắt nhau tại H. Đường thẳng vuông góc với AB tại A cắt BE ở K. Chứng minh rằng DEAK ∽ DECH.

8. Cho tam giác ABC có BC = a, AC = b, AB = c và a² = bc. Chứng minh rằng tam giác ABC đồng dạng với tam giác có độ dài các cạnh bằng độ dài ba đường cao của tam giác ABC.

9. Cho tứ giác ABCD có AB = 1,5cm, BC = 2,5cm, CD = 6cm,
AD = 5cm, AC = 3cm. Chứng minh rằng tứ giác ABCD là hình thang.

10. Cho ABC  có AB = 4cm, AC = 6cm, BC = 9cm. Gọi h₁, h₂, h₃ là chiều cao tương ứng với các cạnh BC, AC, AB. Chứng minh rằng ABC đồng dạng với tam giác có ba cạnh bằng h₁, h₂, h₃.

11. Cho tứ giác ABCD có AB = 8cm,BC = 4cm, CD = 20cm, AD = 25cm, AC = 10cm. Chứng minh tứ giác ABCD là hình thang.