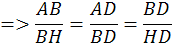Học Để Thi: Giải Toán 9

Bài Tập Toán Thực Tế 9 - Phần Lượng Giác

6:30:00 PM Được đăng bởi Jane Wilde

Giải:

ở đây ta thấy đề cho dữ liệu làm khó học sinh, không chung hình tam giác để áp dụng lượng giác ngay được nên mình phải đưa nó về cùng 1 tam giác.

Xét tam giác AHB, ta có:

HB=AH:tan 60^o=120:√3=40√3

Xét tam giác ACH, ta có:

HC=AH:tan 45^o=AH:1=AH=120

Vậy chiều dài cây cầu:

BC = HC – HB = 120 - 40√3 = 50,72 (m)

Read More Add your Comment 0 nhận xét

Bài toán thực tế lớp 9 - Phần tính tiền lương.

5:47:00 PM Được đăng bởi Jane Wilde

Đề: một xí nghiệp tính lương cho công nhân theo giơ lao động là 25.000 đồng/1 giờ và theo luạt lao động mỗii ngày công nhan làm 8 giờ và dược nghỉ vào ngày chủ nhật hàng tuần. Nếu trong ngày công nhân làm hơn 8 giờ thì số giờ hơn đó công nhan được tính vào giờ tăng ca, mỗi giờ tăng ca được hưỡng 150% tiền lương so với giờ làm viẹc bình thường, làm việc vào ngày chủ nhật thì tính theo giờ tăng ca.

a) Trong tháng 10 có 31 ngày và co1 4 ngày chủ nhật. Xí nghiệp yêu cầu công nhân làm việc một ngày 10 giờ và dược nghỉ vào các ngày chủ nhật. Tính tiền lương công vào tháng 10.

b) Trong tháng 11 có 30 ngày và có 5 ngày chủ nhật. Trong tháng này công nhân có tăng ca trong những ngày bình thường với số giờ tăng ca như nhau ngoài ra công nhân còn làm việc hết tất cả các ngày chủ nhật (mỗi ngày làm 8 giờ) do đó mỗi công nhân nhận được số tiền lương là 9.312.500 đồng. Hỏi những ngày bình thường xí nghiệp tăng ca bao nhiêu giờ?

Giải:

Câu b) đọc đề xong ta thấy tiền lương được tính như sau:

Tiền lương = T_thường.25000+(T_tăng
ca +T_{chủ nhật}).25000.150%

(trong đó T - Time – thời gian )

Trong biểu thức trên:

ü Tiền lương : đề cho.

ü T_{chủ nhật} ,T_thường: tính được

ü T_{tăng ca} : đặt x.

Ở trên là định hướng giải, lúc đọc đề xong có được những định hướng đó thì xem như mình hiểu bài.

Bắt đầu giải:

Cách 1: giải theo lời văn, đi tìm tiền công nhân nhận được khi tăng ca.

Số tiền công nhân làm giờ thường tháng 11là:

(30-5).8.25000=5000000

Số tiền công nhân làm ngày chủ nhật tháng 11 là:

5.8.25000.150%=1500000

Số tiền công nhân nhận được của giờ tăng ca:

9312500-5000000-15000000=2812500 đồng.

Số giờ tăng ca là:

T_{tăng ca}.25000.150%=2812500

=> T_{tăng ca}=75 giờ.

Vậy mỗi ngày công nhân tăng ca thêm: 75:25=3 giờ.

Cách 2: gọi x.

Gọi x là thời gian tăng ca hàng ngày tháng 11.

Tiền lương = T_thường.25000+(T_tăng
ca +T_{chủ nhật}).25000.150%

9312500=(30-5).8.25000+(x.25+8.5).25000.150%

ó(x.25+8.5).37500=9312500-5000000=4312500

ó25x+40=115

ó25x=75

óx=3.

Còn đây là hình Thầy nhận được của đề, nếu có gì sai xót thì xem hình này.

Read More Add your Comment 0 nhận xét

Bài toán thực tế lớp 9 - Phần Trăm

2:56:00 PM Được đăng bởi Jane Wilde

Năm trước Bà Sen mua một khu đất hình chữ nhật có kích thước 4m x 20m. Năm nay Bà Sen bán khu đất đó được 4.000.000.000 đồng và ước tính đạt lợi nhuận 25%. Hỏi năm trước giá bán của 1m2 đất là bao nhiêu.

Giải:

Câu 3:

Mình dùng công thức T.(1+a)=G. Trước đó, Thầy có đưa công thức T.(1-a)=G. Hai công thức này để tính khi có phần trăm rất hay. Nếu T<G dùng Cộng, còn T>G dùng Trừ nha.

Giá miếng đất năm ngoái là: (giá năm ngoái là T, giá hiện tại là G)

T(1+25%)=4.000.000.000

ð T=4.000.000.000:1,25=3.200.000.000 đồng

Giá của 1m2 đất là:

3.200.000.000/80=40.000.000 đồng.

Giải:

Ta thấy T<G nên dùng công thức T.(1+a)=G .

Có 2 cách giải bài này, Thầy làm cả 2 cách:

Các 1: (làm theo lời giải, đi ngược về).

Số tiền trong ngân hàng của Chú Năm sau khi rút 40.000.000 là:

T.(1+9,5%)=194910000

=>T=194910000:1,095=178.000.000

Số tiền trong ngân hàng của chú năm nếu không rút là:

178.000.000+40.000.000=218.000.000

Số tiền ban đầu chú năm gửi là:

T.(1+9%)=218.000.000

T=218.000.000/1,09=200.000.000 đồng.

Cách 2: (gọi x, tìm x)

Gọi x là số tiền ban đầu Chú Năm gửi.

Theo đề bài, ta có:

[x.(1+9%)-40000000].(1+9,5%)=194910000

ó x.1,09 - 40000000=194910000:1,095=178000000

óx.1,09=178000000+40000000=218000000

óx=218000000/1,09=200000000.

d9áp số: 200.000.000 đồng.

Read More Add your Comment 0 nhận xét

Hình Học 9 - HKII - VĨnh Lộc A

9:42:00 PM Được đăng bởi Trang Ánh Nam

Cho (O;R) và một điểm S nằm ngoài đường tròn. Kẻ tiếp tuyến SA với (O) (A là tiếp điểm) và cát tuyến SCD (SD>SC).

a) Chứng minh: SA²=SC.SD

b) Đường thẳng qua A và vuông góc với SO tại I cắt (O) tại B. Chứng minh SC.SD=SI.SO và SB là tiếp tuyến của (O).

c) Gọi F là trung điểm CD; OF cắt AB tại T. Chứng minh 4 điểm T,F,I,S cùng thuộc một đường tròn.

d) Chứng minh: TC²=TF.TO và TC là tiếp tuyến của O.

Giải:

Ta có:

Tứ giác TFIS nội tiếp (chứng minh trên)

=>OF.OT=OI.OS (tự chứng minh)

Lại có: OI.OS=AO²=R²

=>OF.OT=R²=OC²

Mà : hai tam giác CTF và CTO có chung góc T

Suy ra: tam giác CTF đồng dạng với OTC

=>TC² =TF.TO và TC⊥OC (vì F=C=90^o là hai góc tương ứng)

Mà đề cho C thuộc (O) nên TC là tiếp tuyến của (O).

Read More Add your Comment 1 nhận xét

Chứng minh ba điểm thẳng hàng hay

10:28:00 PM Được đăng bởi Trang Ánh Nam

từ điểm A ở ngoài đường tròn (O) vẽ hai tiếp tuyến AB ,AC đến đường tròn (B,C tiếp điểm) Vẽ đ/kính CD (O). Đoạn thẳng AD cắt (O) tại E (E khác D) Vẽ OI vuông với DE tại I.
CM
a) ABOC và ABIO nội tiếp
B) AB^2 = AE.AD
C) Tia OI cắt BC tại F. Cm : FD tiếp tuyến đường tròn (O)
D) Vẽ đường kính EH (O) CM: B,I,H thẳng hàng

Giải câu d:

Ta có:

HB⊥BE (tam giác ABE nội tiếp đường tròn đường kính HE) (*)

Lại có:

ABIOC nội tiếp đường tròn đường kính AO (vì các góc ABO=ACO=AIO=90^o )

=>góc BCO = góc BIF (góc ngoài bằng góc chắn cung đối diện)

Mà góc BED= góc BCD

Suy ra: góc BIF = góc BEI

Vậy ta có:

Góc BEI + góc BIE =góc BFI+góc BIE =90^o (vì góc FIE =90^o )

=>BI⊥BE (**)

Từ (*) và (**) suy ra: BI≡BH (cùng vuông với BE ở B)

Kết luận: B, I,H thẳng hàng.

Read More Add your Comment 0 nhận xét

CHứng minh 3 điểm thẳng hàng của Anh Duy

12:30:00 PM Được đăng bởi Trang Ánh Nam

Cho đường tròn (O;R) và một điểm M nằm ngoài đường tròn (O). Vẽ tiếp tuyến MA của đường tròn (O) với A là tiếp điểm. Vẽ dây cung AC của đuờng tròn tâm (O) vuômg góc với MO tại H
a' Chứng minh: H là trung điểm của AC
b' Chứng minh: MC là tiếp tuyến của (O)
c' Trên tia đối của AC lấy điểm Q. Từ Q vẽ hai tiếp tuyến QD và QE của đuờng tròn (O) với D và E là hai tiếp điểm. Chứng minh ba điểm M, E và D thẳng hàng.

Giải:

Gọi I là giao điểm của ED và QO.

=>DE ⊥QO tại I (1)

Áp dụng hệ thức lượng trong tam giác vuông OAM:

OA²=OH.OM

=>R²=OH.OM (*)

Áp dụng hệ thức lượng trong tam giác vuông OEQ:

OE=OI.OQ

=>R²=OI.OQ (**)

Từ (*) và (**) suy ra: OH.OM = OI.OQ

Mà hai tam giác QOH, MOI có chung góc O.

Nên: QOH đồng dạng với MOI

ð Góc QHO=góc MIO=90^o

ð MI⊥QO (2)

Từ (1) và (2) suy ra MI≡DE (cùng vuông góc với QO)

Vậy M,D,E thẳng hang.

Read More Add your Comment 0 nhận xét

Cho 2 đường tròn O,O’ CẮT nhau ở A,B (O Ó thuộc mặt phẳng A,B).Kẻ các đường kính góc BOC và góc BO’C. Chứng minh C,A,D thẳng hàng, Cho OO=5,OB=4,ÓB=3 tính diện tích tam giác BCD

10:26:00 AM Được đăng bởi Trang Ánh Nam

Cho 2 đường tròn O,O’ CẮT nhau ở A,B (O Ó thuộc mặt phẳng A,B).Kẻ các đường kính góc BOC và góc BO’C. Chứng minh C,A,D thẳng hàng, Cho OO=5,OB=4,ÓB=3 tính diện tích tam giác BCD

Giải:

Ta có:

ü CA⊥AB (vi góc CAB là góc nội tiếp chắn nữa đường tròn O)

ü DA⊥AB(vi góc DAB là góc nội tiếp chắn nữa đường tròn O’)

Vậy hai đường thẳng CA ,DA trùng nhau (cùng vuông vối AB tại A)

=>C, A, D thẳng hàng

* Tính Diện tích tam giác BCD:

Đầu tiên ta thấy: 5²=4²+3²

=>OO’²= OB² +O’B²

=> tam giác OO’B vuông tại B, cũng suy được tam giác BCD vuông tại B.

Vậy ta sẽ tính diện tích tam giác đựa vào hai cạnh góc vuông:

S_BCD=1/2.BC.BD=1/2.2BO.2BO’=2BO.BO’=2.3.4=24

Read More Add your Comment 0 nhận xét

Hướng dẫn giải Hình Học cho bạn đọc giấu tên

12:01:00 AM Được đăng bởi Trang Anh Nam

Cho tam giác ABC cân tại A có các đường cao AD và BE cắt nhau tại H. Biết AC = 10 và BC = 12, tính HD, HA, HB, HE

Giải:

Theo tính chất tam giác cân thì D là trung điểm BC nên BD=CD=6

Áp dụng Pitago vào tam giác vuông ABD ta được:

AD²=AB²-BD²=10²-6²=64 =>AD=8

ở đây do em không nói học lớp mấy nên T sẽ giải theo 2 cách:

ü Cách 1: dành cho Học Sinh lớp 8.

Lớp 8 thì ta dùng tam giác đồng dạng:

Xét 2 tam giác vuông ABD và BDH:

Ta có:

v (tam giác AHF vuông tai F)

v (Tam giác ABD vuông tại D)

Mà: (đối đỉnh)

Suy ra:

Vậy: ABD BHD

=>BH=10.6/8=7.5, HD=6.6/8=4.5

=>HA=AD-HD=8-4,5=3,5

Dể dàng chứng minh được: BHDAHE

ü Cách 2: dung cho học sinh lớp 9:

ở lớp 9 thì e vẫn có thể dung cách của lớp 8 như trên, hoạc dung cách của lớp 9 là "Lượng giác" tức là dùng sin, cos, tan, cot

ở đây T chỉ hướng dẫn cách làm chứ ko gaii3 chi tiết.

đầu tiên tính AD, tiếp theo là tính HD, sau đó tính HA rồi tính các cạnh còn lại. Cố gắng lên nhé. Chúc em thành công.

Read More Add your Comment 0 nhận xét

Hướng dẫn giải toán 9 - Hùng 9C

10:10:00 PM Được đăng bởi Trang Anh Nam

thầy ơi giải júp bài toán này:cho phương trình:x^2-(3m-1)x+2m^2-m=0
A, Giải phương trình với m=1
B, Tìm m để phương trình có 2 nghiệm phân biệt x1,x2 thỏa mãn /x1-x2/-2
Mong thầy giải jup em bài này.

Giải:

x² – (3m-1)x +2m² – m =0

a. Với m=1 phương trình trở thành:

X² - 2x + 1 =0

=>(x-1)²=0

=>x-1=0

=>x=1

b. câu b em viết không rỏ, T sẽ giải theo suy nghĩ của T, đề sẽ như sau:

Tìm m để phương trình có 2 nghiệm phân biệt x1,x2 thỏa mãn: |x₁-x₂|=2

|x₁-x₂|=2, ở đây ta sẽ dùng Vi-et để giải, nhưng Vi-et thì phải có S,P. Nên việc của mình là làm cho hai anh này xuất hiện, bằng cách bình phương hai ve của phương trình trên.

(|x₁-x₂|)²=2²

<=> x₁²-2x₁x₂+x₂²=4

<=> x₁²+2x₁x₂+x₂²-4x₁x₂=4

<=> (x₁+x₂)²-4x₁x₂=4 (*)

Và bay giờ mọi chuyện trỏ nên dể dàng:

Áp dụng Vi-et vào phương trình đầu bài ta có:

S=x₁+x₂= = 3m-1