TRƯỜNG ĐẠI HỌC SÀI GÒN                                         KÌ THI KẾT THÚC HỌC PHẦN

        KHOA TOÁN - ỨNG DỤNG                                        HỌC KỲ I - NĂM HỌC 2011 - 2012

ĐỀ THI HỌC PHẦN: QUY HOẠCH TUYẾN TÍNH. ĐỀ SỐ: 01.

DÀNH CHO LỚP: DKE1101-1102-1103.

THỜI GIAN LÀM BÀI: 90 phút (Không kể thời gian phát đề).

Câu 1: (6đ)  Một xí nghiệp sản xuất hai loại sản phẩm A và B từ ba loại nguyên liệu C, D và E với số lượng dự trữ lần lượt là 100, 82 và 120 đon vị. Để sản xuất ra mỗi đơn vị sản phẩm loại A cần sử dụng 4 đơn vị nguyên liệu C, 4 đơn vị nguyên liệu D và 6 đơn vị nguyên liệu E. Các chỉ số đó cho mỗi đơn vị sản phẩm B theo thứ tự trên là 6, 3 và 4. Do điều kiện thực tế, xí nghiệp bắt buộc phải sử dụng hết 120 đơn vị nguyên liệu loại E hiện có. Cho biết lợi nhuận thu được trên mỗi sản phẩm loại A và loại B lần lượt là 4 triệu đồng và 6 triệu đồng.

1.     Hãy thiết lập kế hoạch sản suất nhằm đạt tổng lợi nhuận tối đa và tìm phương án sản xuất tối ưu bằng phương pháp thích hợp.

2.     Viết bài toán đối ngẫu của bài toán trên và tìm phương án tối ưu của nó.

Câu 2: (4đ) Cần vận chuyển một loại hàng từ ba kho hàng đến bốn nơi tiêu thụ (cửa hàng). Số lượng đơn vị hàng ở các kho tương ứng là , số lượng đơn vị hàng cần có ở các cửa hàng là  và cước phí vận chuyển một đơn vị hàng từ kho thứ i đến cửa hàng thứ j cho bởi ma trận sau:

Hãy lập kế hoạch vận chuyển hàng sao cho đảm bảo cung cầu và cước phí vận chuyển nhỏ nhất (phương án tối ưu).

.....................................................................................................................................................................

HẾT

TRƯỜNG ĐẠI HỌC SÀI GÒN                                               KÌ THI KẾT THÚC HỌC PHẦN

        KHOA TOÁN - ỨNG DỤNG                                        HỌC KỲ I - NĂM HỌC 2011 - 2012

ĐỀ THI HỌC PHẦN: QUY HOẠCH TUYẾN TÍNH. ĐỀ SỐ: 02.

DÀNH CHO LỚP: DKE1101-1102-1103.

THỜI GIAN LÀM BÀI: 90 phút (Không kể thời gian phát đề).

Câu 1: (6đ)  Xí nghiệp sản xuất giấy có 3 phân xưởng. Do trang bị kỹ thuật khác nhau nên mức hao phí tre gỗ, axit để sản xuất một tấn giấy thành phẩm cũng khác nhau. Mức hao phí được cho trong bảng dưới đây:

Số lượng tre gỗ có trong năm là 1.500.000 tấn, Axit là 100.000 tấn. Yêu cầu: 

1.     Xây dựng mô hình sao cho tổng số giấy sản xuất trong năm của xí nghiệp là nhiều nhất.

2.     Xây dựng mô hình bài toán đối ngẫu với mô hình toán của 1.

3.     Tìm phương án tối ưu ứng với mô hình toán ở 1. Từ đó suy ra số tấn giấy của mỗi phân xưởng cần sản xuất trong năm.

4.     Áp dụng kết quả bài toán đối ngẫu để từ bảng đơn hình tối ưu 3. suy ra phương án tối ưu cho bài toán đối ngẫu 2.

Câu 2: (4đ) Một công ty có ba xí nghiệp cùng sản xuất một loại sản phẩm. Năng suất trong tháng của ba xí nghiệp lần lượt là  sản phẩm. Hợp đồng công ty phải giao cho bốn nhà phân phối là  sản phẩm. Đơn giá (đơn vị tính: 1000 đồng) của mỗi sản phẩm tương ứng với các nhà phân phối được cho bởi ma trận sau:

Hãy lập kế hoạch vận chuyển hàng sao cho đảm bảo cung cầu và cước phí vận chuyển nhỏ nhất (phương án tối ưu).

.....................................................................................................................................................................

HẾT

Câu 1.

1.     Gọi : là số lượng sản phẩm loại j của xí nghiệp sản xuất, j=A,B.

Ta có mô hình bài toán:

.

Ta có bảng đơn hình

Ta có các , do đó phương án tối ưu của bài toán:

          và

2.     Gọi : là giá trị của nguyên vật liệu thứ i (i=C, D, E).

Ta có mô hình bài toán:

Từ bảng đơn hình ta có kết quả của bài toán đối ngẫu, như sau:

và .

Câu 2.

·        Kiểm tra điều kiện cân bằng thu phát, ta có .

·        Xây dựng phương án ban đầu:

·        Kiểm tra tính tối ưu, ta thấy .

·        Xây dựng phương án mới:

·        Kiểm tra tính tối ưu, ta thấy . Ta có phương án tối ưu của bài toán:

, và đơn vị tiền tệ.

Câu 1.

1.     Gọi : là số lượng giấy do phân xưởng thứ j sản xuất, j=1,2,3.

Ta có mô hình bài toán:

.

2.     Gọi : là giá trị của tre gỗ và axit.

Ta có mô hình bài toán:

3.     Giải bài toán 1 bằng phương pháp đơn hình

4.     Từ bảng đơn hình ta có kết quả của bài toán 2, như sau:

và .

Câu 2.

·        Kiểm tra điều kiện cân bằng thu phát, ta có .

·        Ta thêm một trạm phát giả  và .

·        Xây dựng phương án ban đầu:

·        Kiểm tra tính tối ưu, ta thấy .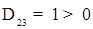

·        Xây dựng phương án mới:

Kiểm tra tính tối ưu, ta thấy .