Chương IV. BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN

§1. LIÊN HỆ GIỮA THỨ TỰ VÀ PHÉP CỘNG.
LIÊN HỆ GIỮA THỨ TỰ VÀ PHÉP NHÂN

A/ KIẾN THỨC VÀ KĨ NĂNG CẦN NHỚ

I. Liên hệ giữa thứ tự và phép cộng :

1. Bất đẳng thức : Ta gọi hệ thức dạng a < b (hay a > b, a £ b, a ³ b) là bất đẳng thức và gọi a là vế trái, b là vế phải của bất đẳng thức.

Ta gọi hệ thức dạng a < b (hay a > b, a £ b, a ³ b) là bất đẳng thức và gọi a là vế trái, b là vế phải của bất đẳng thức.

2. Liên hệ giữa thứ tự và phép cộng

Tính chất. Khi cộng cùng một số vào cả hai vế của một bất đẳng thức ta được bất đẳng thức mới cùng chiều với bất đẳng thức đã cho.

II. Liên hệ giữa thứ tự và phép nhân

1. Liên hệ giữa thứ tự và phép nhân với số dương

Tính chất : Khi nhân cả hai vế của một bất đẳng thức với cùng một số dương ta được bất đẳng thức mới cùng chiều với bất đẳng thức đã cho.

2. Liên hệ giữa thứ tự và phép nhân với số âm

Tính chất : Khi nhân cả hai số của một bất đẳng thức với cùng một số âm ta được bất đẳng thức mới ngược chiều với bất đẳng thức đã cho.

3. Tính chất bắc cầu của thứ tự : Với ba số a, b, c ta có: nếu a < b và b < c thì a < c.

B/ BÀI TẬP :

& BÀI TẬP CƠ BẢN

91. Cho x > y, hãy so sánh :

a) x + 2009 và y + 2009                 b) x – 2010 và y – 2010                      c) x + y và 2y

92. Hãy so sánh m và n nếu :

a) m + 2009 ³ n + 2009                  b) m – 2009 £ n – 2009.

93. Cho x £ y, hãy so sánh :

a) 2009x và 2009y                          b) 69x – 7 và 69y – 7

c) –60x và –60y                              d) –75x + 8 và –75y + 8.

94. Cho m > n. Chứng minh rằng :

a) m + 2009 > n + 2007                  b) 8m – 5 > 8n – 5                               c) 9m + 2 > 9n – 1.

95. Chứng minh :

a) 20(–11) + 2009 < 20(–10) + 2009                      b) (–30)4 + 75 < (–30) (–4) + 75

96. Cho a < b. chứng minh :

a) 8a + 5 < 8b + 5                                                   b) –9a – 34 > –9b – 34.

97. So sánh m và n nếu :

a) m + 4 ³ n + 4                                                      b) –6m £ –6n

c) 5m – 8 > 5n – 8                                      d) –2m – 7 < –2n – 7.

98. Cho p > q, hãy so sánh :

a) –3000p và –3000q                      b) 500p – 9 và 500q – 9                      c) 45p + 96 và 45q + 95.

99. So sánh số x và số 0 nếu :

a) 7x < 9x                                       b) 8x < 7x                                c) –5x > –9x.

& BÀI TẬP TRẮC NGHIỆM

100. Chọn câu trả lời đúng :

Xét các khẳng định sau : (I) x – 472 ³ y – 472 nếu x ³ y ; (II) x ³ y nếu x – 472 ³ y – 472.

A. Chỉ có (I) đúng                                                  B. Chỉ có (II) đúng

C. Cả (I) và (II) đúng                                             D. Cả (I) và (II) sai.

& BÀI TẬP NÂNG CAO

101. Chứng minh rằng :

a) a² + b² ³ 2ab                                           b) (a + b)² ³ 4ab                      c) 2(a² + b²) ³ (a + b)²

d) (ax + by)² £ (a² + b²) (x² + y²)                e) a² + b² + c² + d² + e² ³ a(b + c + d + e)

f) a² + b² + c² ³ ab + bc + ca.

102. Cho a, b, c > 0. Chứng minh rằng :

a)  ³ 2                                              b) a³ + b³ ³ a²b + ab²               c)  ³ a + b + c

d)  ³ a + b + c                       e)

f)  £ 3(a + b + c).

103. Cho a, b, c là độ dài ba cạnh của một tam giác. Chứng minh rằng :

a) a² + b² + c² < 2(ab + bc + ca)                             b) (a + b + c)(a – b + c)(–a + b + c) £ abc

& BÀI THI CHỌN HỌC SINH GIỎI TOÁN

104. a) Chứng minh các bất đẳng thức sau :

1) (a² + b²)(a² + 1) ³ 4a²b, với mọi a, b.                 2) , với mọi a, b > 0

3)  

(Đề thi chọn HSG Toán 8, Trường THCS Hoa Lư, Quận 9 – TP. Hồ Chí Minh, năm học 2000 – 2001)

b) 1) Chứng minh bất đẳng thức : a² + b² + c² ³ ab + bc + ac

2) Cho a, b, c là ba số dương. Chứng minh :  

(Đề thi chọn HSG Toán 8, Trường Nguyễn Du, Quận 1 – TP. Hồ Chí Minh, năm học 2001 – 2002)

c) Cho a ³ b ³ c > 0. Chứng minh bất đẳng thức :  

(Đề thi chọn học sinh giỏi Toán lớp 8, Quận 6 – TP. Hồ Chí Minh, năm học 1998 – 1999)

105. a) Cho ba số a, b, c sao cho : 0 £ a £ 2, 0 £ b £ 2, 0 £ c £ 2 và a + b + c = 3.

Chứng minh rằng a² + b² + c² £ 5

(Đề thi chọn học sinh giỏi Toán lớp 8, Quận 6 – TP. Hồ Chí Minh, năm học 1998 – 1999)

b) Cho x, y là số dương thoả mãn x³ + y⁴ £ x² + y³. Chứng minh rằng :

       1. x³ + y³ £ x² + y²                             

2. x² + y³ £ x + y²

(Đề thi chọn học sinh giỏi Toán lớp 9, Quận 1 – TP. Hồ Chí Minh, năm học 2004 – 2005)

c) Cho a³ + b³ = 2. Chứng minh rằng 0 < a + b £ 2.

(Đề thi vào lớp 10 chuyên Toán,Trường THPT chuyên Lê Hồng Phong,TP.HCM, năm học 2008 – 2009)

§2. BẤT PHƯƠNG TRÌNH MỘT ẨN. BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN

A/ KIẾN THỨC VÀ KĨ NĂNG CẦN NHỚ

I. Bất phương trình bậc nhất một ẩn

1. Mở đầu

– Ta gọi hệ thức 16x + 5 ³ 70 (1) là một bất phương trình với ẩn là x; trong đó 16x + 5 là vế trái và 70 là vế phải của bất phương trình.

– Khi thay giá trị x = 5 vào (1), ta được: 16.5 + 5 ³ 70 là khẳng định đúng. Ta nói số 5 (hay giá trị x = 5) là một nghiệm của bất phương trình (1).

– Khi thay x = 2 vào (1), ta được: 16.2 + 5 ³ 75 là khẳng định sai. Ta nói số 2 (hay giá trị x = 2) không phải là nghiệm của bất phương trình (1).

2. Tập nghiệm của bất phương trình

– Tập hợp tất cả các nghiệm của một bất phương trình được gọi là tập nghiệm của bất phương trình.

– Giải bất phương trình là tìm tập nghiệm của bất phương trình đó.

Ví dụ 1: Bất phương trình x > 3 có tập nghiệm là {x | x > 3}. Tập hợp này được biểu diễn trên trục số như hình vẽ bên.

Ví dụ 2: Bất phương trình x £ 2 có tập nghiệm là {x | x £ 2}. Tập hợp này được biểu diễn trên trục số như hình vẽ bên.

3. Bất phương trình tương đương

Hai bất phương trình có cùng tập nghiệm là hai bất phương trình tương đương và dùng kí hiệu "Û" để chỉ sự tương đương đó. Ví dụ 3: x £ 2 Û 2 ³ x.

II. Bất phương trình bậc nhất một ẩn

1. Định nghĩa

Bất phương trình dạng ax + b < 0 (hoặc ax + b > 0, ax + b £ 0, ax + b ³ 0) trong đó a và b là hai số đã cho, a ¹ 0, được gọi là bất phương trình bậc nhất một ẩn.

2. Hai quy tắc biến đổi bất phương trình

a) Quy tắc chuyển vế: Khi chuyển một hạng tử của bất phương trình từ vế này sang vế kia ta phải đổi dấu hạng tử đó.

b) Quy tắc nhân với một số: Khi nhân hai vế của bất phương trình với cùng một số khác 0, ta phải:

– Giữ nguyên chiều bất phương trình nếu số đó dương;

– Đổi chiều bất phương trình nếu số đó âm.

3. Cách giải :Bất phương trình bậc nhất một ẩn ax + b < 0 được giải như sau: ax + b < 0 Û ax < –b (1)

· Nếu a > 0 thì (1) Û x < –                                            · Nếu a < 0 thì (1) Û x > –.

Vậy nghiệm của bất phương trình ax + b < 0 là x < – nếu a > 0; x > – nếu a < 0.

B/ BÀI TẬP

& BÀI TẬP CƠ BẢN

106. Viết tập nghiệm của mỗi bất phương trình bằng kí hiệu tập hợp, rồi biểu diễn chúng trên trục số.

a) x < 0                                           b) x > –3.

107. a) Áp dụng quy tắc nhân, giải các bất phương trình sau :

1. 6x < 18                                  2. –3x > 24                  3. –6x £ –90                4. 8x ³ –40.

b) Áp dụng quy tắc nhân, giải các bất phương trình sau :

1. x < 4                       2. –x >                           3. x £                 4. –x ³ –.

108. Giải thích sự tương đương sau :

a) x – 7 < 9 Û x + 3 < 19                          b) –5x ³ 3 Û 20x £ –12.

109. Các bất phương trình sau có tương đương không ? Vì sao ?

a) x – 5 > 0 và –2x < –10               b) –2x – 6 < 5 – 3x và êx ê < 11.

110. Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số

a) 3x – 7 > 23                                             c) –2 – 2x £ –10

b) 5x – 9 < 6                                               d) 3 – 10x ³ 33.

111. Cho bất phương trình (x – 3)² > 0 (1)

a) Chứng minh rằng : x = 4 ; x = –1 ; x = –3 là các nghiệm của bất phương trình (1).

b) Có thể kết luận rằng với mọi giá trị của ẩn số x đều là nghiệm của bất phương trình (1) hay không ?

112. Hình vẽ sau biểu diễn tập nghiệm của bất phương trình nào ? (Viết ra hai bất phương trình có cùng tập nghiệm)

113. Tìm giá trị của x sao cho :

a) Giá trị của biểu thức 5x – 8 không âm. b) Giá trị của biểu thức –3x + 5 không dương.

114. Giải các bất phương trình và biểu diễn tập nghiệm của chúng trên trục số :

a)  < 3                                                       b)  > 5

c)  ³ 7                                                          d)  ³ .

& BÀI TẬP TRẮC NGHIỆM

115. Chọn câu trả lời đúng :

Hình vẽ nào dưới đây biểu diễn tập nghiệm của bất phương trình x £ –2

A. Hình 1                           B. Hình 2                                C. Hình 3                                D. Hình 4.

& BÀI TẬP NÂNG CAO

116. Giải các bất phương trình sau :

a)  ³ –3                                b)  < 4

c)  > –19.

117. Giải các bất phương trình sau :

a)  >  

b)  £  

c)  < .

118. Giải và biện luận bất phương trình sau : (m + 2)x > (m + 2)(m – 5).

119. Hãy lập bất phương trình của bài toán sau :

Quãng đường AB dài 141 km. Lúc 6 giờ một mô tô khởi hành đi từ A đến B, trong giờ thứ nhất mô tô đi với vận tốc 29 km/giờ. Hỏi trong quãng đường còn lại mô tô phải đi với vận tốc là bao nhiêu để đến B trước 10 giờ 30 phút ?

& BÀI THI CHỌN HỌC SINH GIỎI TOÁN

120. Giải các bất phương trình sau :

a) .

(Đề thi chọn học sinh giỏi Toán lớp 8, Quận Tân Bình – TP. Hồ Chí Minh, năm học 2003 – 2004)

b) x² – 3x > 0.

(Đề thi chọn HSG Toán 8, Trường  Nguyễn Du, Quận 1 – TP. Hồ Chí Minh, năm học 2000 – 2001)

c)  > 2.

(Đề thi chọn HSGToán 8, Trường Nguyễn Gia Thiều, Quận Tân Bình – TP.HCM, năm  2000 – 2001)

§3. PHƯƠNG TRÌNH CHỨA DẤU GIÁ TRỊ TUYỆT ĐỐI

A/ KIẾN THỨC VÀ KĨ NĂNG CẦN NHỚ

Cách giải phương trình dạng ½A½ = B

Cách 1 :      ½A½ = B Û 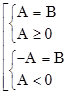                      Cách 2 :          ½A½ = B Û

· Chú ý : Nếu việc giải bất phương trình trong hệ quá phức tạp thì ta chỉ cần giải phương trình trong hệ, rồi thử các giá trị vừa tìm được của ẩn có thoả mãn bất phương trình trong hệ hay không. Từ đó xác định được nghiệm của phương trình ½A½ = B.

B/ BÀI TẬP

& BÀI TẬP CƠ BẢN

121. Bỏ dấu giá trị tuyệt đối và rút gọn biểu thức :

a) A = 5x – 9 + ½3x½ trong hai trường hợp : x ³ 0 và x < 0

b) B = x – ½8x½ – 26 trong hai trường hợp : x £ 0 và x > 0

c) C = ½x + 5½ + 6x – 5 khi x ³ –5

d) D = ½13 – x½ + x + 13 khi x > 13.

122. Bỏ dấu giá trị tuyệt đối và rút gọn biểu thức :

a) A = 48 + ½2x – 8½ khi x < 4                  b) B = 6x + ½30 – 6x½ khi x > 5.

123. Bỏ dấu giá trị tuyệt đối và rút gọn biểu thức :

a) A = ½x – 7½ + 7                                     b) B = ½9 – 3x½ + 3x.

124. Giải các phương trình :

a)½x½ – 2x = 15                                         b) ½5x½ + 12 = x.

125. Giải các phương trình sau :

a) ½x – 9½ = 2x + 13                                  b) ½x + 5½ = 6x – 25.

126. Giải các phương trình sau :

a) ½x + 8½ = 4x – 10                                  b) ½x – 8½ + 2x = 46.

& BÀI TẬP TRẮC NGHIỆM

127. Chọn câu trả lời đúng :

Tập nghiệm của phương trình 3½x½ = x + 60 là :

A. S = {30}            B. S = {30; –30}                     C. S = {30; –15}                     D. S = {30; 15}.

& BÀI TẬP NÂNG CAO

128. Giải các phương trình sau :

a) ½x – 1½ – 2½x½ = –2                 b) ½x + 1½ + x = ½3x + 2½ + x           c) ½x³ – x – 8½ = x³ + x + 8.

129. Giải các phương trình sau :

a) ½2x – 5½ = ½x + 3½                                b) ½x – 1½ = ½3x + 10½.

130. Giải các phương trình sau :

a) ½x – 7½ = x – 7                                       b) ½x – 9½ = 9 – x

c) ½x – 1½ = ½1 – x½.

131. Giải các phương trình sau :

a) ½x – 5½ + ½x – 2½ = 3                           b) ½2x + 5½ + ½2x – 7½ = 12

c) ½5x – 1½ + ½5x + 7½ = 8.

132. Giải các phương trình sau :

a) ½x + 5½ + ½x + 7½ + ½x + 15½ = 4x

b) ½x + 1½ + ½x + 2½ + ½x + 3½ + ... + ½x + 2009½ = 2010x.

133. Giải các phương trình sau :

a) ½x – 4½²⁰ + ½x – 3½²¹ = 1                      b) ½x – 2009½¹⁹⁶³ + ½x – 2010½¹⁹⁶⁴ = 1.

& BÀI THI CHỌN HỌC SINH GIỎI TOÁN

134. Giải các phương trình sau :

a) ½x² – 5x + 5½ = –2x² + 10x – 11

(Đề thi chọn HSG Toán 8, Trường  Nguyễn Du, Quận 1 – TP. Hồ Chí Minh, năm học 1998 – 1999)

b) ½2x – 1½ – 3½x + 1½ = 2x + 6

(Đề thi chọn học sinh giỏi Toán lớp 8, Quận 6 – TP. Hồ Chí Minh, năm học 1999 – 2000)

c) ½x – 1½ + ½x – 5½ = 4

(Đề thi chọn HSG Toán 8,  Trường  Hoàng Văn Thụ, Quận 10 – TP. HCM, năm học 2001 – 2002)

135. Giải phương trình :

½2x – ½2x – 1½½ = –m²x  (với m là tham số).

(Đề thi chọn HSG Toán  8, Trường  Hoa Lư, Quận 9 – TP. Hồ Chí Minh, năm học 2001 – 2002)