TỨ GIÁC. HÌNH THANG

9:24:00 PM Được đăng bởi Trang Anh Nam

A/ KIẾN THỨC VÀ KĨ NĂNG CẦN NHỚ

I. TỨ GIÁC

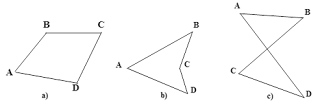
1. Định nghĩa : Tứ giác ABCD là hình gồm bốn đoạn thẳng AB, BC, CD, DA trong đó bất kì hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng (h.a), b), c)).

Ta chỉ xét tứ giác như ở hình a), gọi là tứ giác lồi.

2. Tổng các góc của một tứ giác

Định lí : Tổng các góc của một tứ giác bằng 360^o.

II. HÌNH THANG

1. Định nghĩa :

Hình thang là tứ giác có hai cạnh đối song song.

Nhận xét

– Nếu một hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau, hai cạnh đáy bằng nhau.

– Nếu một hình thang có hai cạnh đáy bằng nhau thì hai cạnh bên song song và bằng nhau.

2. Hình thang vuông

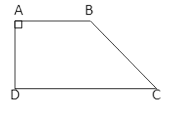Định nghĩa : Hình thang vuông là hình thang có một góc vuông.

B/ BÀI TẬP

& BÀI TẬP CƠ BẢN

1. a) Cho tứ giác ABCD có = 6 : 5 : 4 : 3. Tính các góc của tứ giác ABCD.

b) Cho tứ giác ABCD có = 60⁰, = 120⁰, = 80⁰. Tính số đo góc ngoài tại đỉnh A.

c) Tính tổng các góc ngoài của tứ giác.

d) Chứng minh rằng các góc của tứ giác không thể đều là góc nhọn, không thể đều là góc tù.

2. a) Tính các góc , của hình thang ABCD (AB // CD) biết = 70⁰, = 40⁰.

b) Cho hình thang ABCD có AB // CD và . Chứng minh rằng ABCD là hình thang vuông và AC² + BD² = AB² + CD² + 2AD²

c) Chứng minh rằng trong hình thang có nhiều nhất có hai góc tù, có nhiều nhất là hai góc nhọn.

3. a) Cho hình thang ABCD (AB // CD) có DB là tia phân giác góc D.

Chứng minh rằng AB = AD.

b) Cho tứ giác ABCD có AB = AD, DB là tia phân giác góc D. Chứng minh ABCD là hình thang.

4. Cho hình thang vuông ABCD (AB // CD, = 90⁰, AB < CD). Đường thẳng qua A song song với BC cắt CD ở E.

So sánh AE và BC, AD và BC

& BÀI TẬP TRẮC NGHIỆM

5. Chọn câu trả lời đúng :

Hình thang ABCD (AB // CD) có = 130⁰. Số đo của góc D bằng :

A. 130⁰ B. 50⁰ C. 40⁰ D. Một kết quả khác.

& BÀI TẬP NÂNG CAO

6. Cho tứ giác ABCD có = 180⁰, AB < AD, AC là tia phân giác của . Trên cạnh AD lấy E sao cho AE = AB. Chứng minh rằng BC = CE = CD.

7. Cho tứ giác ABCD.

a) Chứng minh rằng AB + CD < AC + BD

b) Cho biết AB + BD £ AC + CD

Chứng minh rằng AB < AC

8. Cho hình thang ABCD có AC ^ BD. Chứng minh rằng :

a) AB² + CD² = AD² + BC² b) (AB + CD)² = AC² + BD²

9. Cho hình thang ABCD (AB // CD) có AB = AD + BC. Chứng minh rằng các tia phân giác của các góc C, D gặp nhau tại một điểm trên cạnh AB.

& BÀI THI CHỌN HỌC SINH GIỎI TOÁN

10. a) Cho tứ giác ABCD, M là một điểm nằm trong tứ giác ABCD. Xác định vị trí điểm M để MA + MB + MC + MD nhỏ nhất.

(Đề thi giải Lê Quý Đôn Toán lớp 7, báo Khăn Quàng Đỏ, Tp. Hồ Chí Minh, năm c 2007 – 2008)

b) Cho một tứ giác không có hai góc nào bằng nhau. Chứng minh rằng tứ giác ấy có ít nhất một góc nhọn và một góc tù.

(Đề thi giải Lê Quý Đôn Toán lớp 7, báo Khăn Quàng Đỏ, Tp. Hồ Chí Minh, năm 2009 – 20010)

§2. HÌNH THANG CÂN

A/ KIẾN THỨC VÀ KĨ NĂNG CẦN NHỚ

1. Định nghĩa : Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.

2. Tính chất

Định lí 1 : Trong hình thang cân, hai cạnh bên bằng nhau.

Định lí 2 : Trong hình thang cân, hai đường chéo bằng nhau.

3. Dấu hiệu nhận biết hình thang cân

– Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.

– Hình thang có hai đường chéo bằng nhau là hình thang cân.

B/ BÀI TẬP

& BÀI TẬP CƠ BẢN

11. Cho hình thang cân ABCD (AB // CD), O là giao điểm của AC và BD.

Chứng minh rằng :

a) DACD = DBDC

b) OC = OD, OA = OB

12. Cho tam giác ABC vuông tại A. Về phía ngoài tam giác ABC, vẽ tam giác ABD vuông cân tại A, vẽ tam giác ACE vuông cân tại E.

Chứng minh rằng tứ giác BDEC là hình thang cân.

13. Cho hình thang cân ABCD (AB // CD) có AB = BC, AB < CD.

Chứng minh rằng CA là tia phân giác của góc BCD.

14. Cho tam giác ABC cân tại A. Lấy D trên cạnh AB, E trên cạnh AC sao cho AD = AE. Chứng minh rằng BDEC là hình thang cân.

15. Cho tam giác đều ABC. M là điểm nằm trong tam giác ABC. Đường thẳng qua M song song với BC cắt AB ở D, đường thẳng qua M song song với AC cắt BC ở E, đường thẳng qua M song song với AB cắt AC ở F.

Chứng minh rằng :

a) Các tứ giác ADMF, BDMF, CFME là các hình thang cân

b) ½MB – MC½ < MA < MB + MC

& BÀI TẬP TRẮC NGHIỆM

16. Chọn câu trả lời đúng :

Cho hình thang cân ABCD (AD // BC) có = 100⁰. Số đo của góc D bằng :

A. 80⁰ B. 50⁰

C. 100⁰ D. Một kết quả khác.

& BÀI TẬP NÂNG CAO

17. Cho hình thang cân ABCD (AB // CD). Chứng minh rằng AB + CD < 2AC

18. a) Cho tứ giác ABCD có , BC = AD. Chứng minh rằng ABCD là hình thang cân.

b) Cho tứ giác ABCD có = 180⁰, AB = BC = AD. Chứng minh rằng ABCD là hình thang cân.

19. Cho hình thang ABCD (AB // CD) có . Chứng minh rằng AC > BD.

& BÀI THI CHỌN HỌC SINH GIỎI TOÁN

20. Cho góc xOy có số đo bằng 60⁰. Trên hai tia Ox, Oy lần lượt lấy các điểm tùy ý B và C.

Chứng minh rằng OB + OC £ 2BC

(Đề thi chọn học sinh giỏi Toán lớp 8, trường THCS Nguyễn Du, Quận 1, Tp. Hồ Chí Minh, năm học 1998 – 1999)

§3. ĐƯỜNG TRUNG BÌNH CỦA TAM GIÁC,
CỦA HÌNH THANG

A/ KIẾN THỨC VÀ KĨ NĂNG CẦN NHỚ

1. Đường trung bình của tam giác

Định lí 1 : Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.

Định nghĩa : Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.

Định lí 2 : Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.

2. Đường trung bình của hình thang

Định lí 3 : Đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm cạnh bên thứ hai.

Định nghĩa : Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang.

Định lí 4 : Đường trung bình của hình thang thì song song với hai đáy và bằng nửa tổng hai đáy.

B/ BÀI TẬP

& BÀI TẬP CƠ BẢN

21. Cho tam giác ABC vuông tại A. M là trung điểm cạnh BC. Vẽ
MN ^ AB tại N. Chứng minh rằng N là trung điểm đoạn thẳng AB.

22. Cho tam giác ABC cân tại A. Gọi D, E lần lượt là trung điểm của các cạnh AB, AC. Chứng minh rằng BDEC là hình thang cân.

23. Cho hình thang ABCD (AB // CD). Gọi M, N, K lần lượt là trung điểm của các đoạn thẳng AD, BC, AC. Chứng minh rằng MK // AB ; M, N và K thẳng hàng.

24. Cho tam giác ABC có BD và CE là hai đường trung tuyến cắt nhau tại G. Gọi M, N lần lượt là trung điểm của các đoạn thẳng GB, GC.

Chứng minh rằng DE // MN, DE = MN

& BÀI TẬP TRẮC NGHIỆM

25. Chọn câu trả lời đúng :

Tính x, y trên hình bên trong đó AB // CD // EF // MN, AE = EM = MD.

A. x = 14 cm ; y = 22 cm

B. x = 12 cm ; y = 22 cm

C. x = 14 cm ; y = 20 cm

D. x = 14 cm ; y = 24 cm.

& BÀI TẬP NÂNG CAO

26. Cho tam giác ABC vuông tại A. Vẽ AH ^ BC tại H. Gọi M, N lần lượt là trung điểm của các đoạn thẳng AH, CH. Chứng minh rằng MN ^ AB và BM ^ AN.

27. Cho tam giác ABC. Các điểm D, E lần lượt trên các cạnh BC, AB sao cho BD = CD, BE = 2AE. Gọi M là giao điểm của AD và CE. Chứng minh rằng MA = MD.

28. Cho hình thang vuông ABCD

( = 90⁰). M là trung điểm cạnh BC. Chứng minh rằng tam giác MAD cân.