OÂN TAÄP CHÖÔNG III

70. Cho tam giaùc ABC coù AB = 9cm, AC = 12cm. Caùc ñieåm D, E laàn löôït treân caùc caïnh AB, AC sao cho : AD = 3cm, AE = 4cm.

a) Chöùng minh raèng : DE // BC.

b) M laø ñieåm treân caïnh BC sao cho BM = 2,5MC. Goïi N laø giao ñieåm cuûa AM vaø DE.

Chöùng minh raèng DN = 2,5NE.

71. Cho hình thang ABCD (AB // DC). E laø giao ñieåm cuûa AD vaø BC, F laø giao ñieåm cuûa AC vaø BD. Chöùng minh raèng ñöôøng thaúng EF ñi qua trung ñieåm cuûa AB vaø qua trung ñieåm cuûa DC.

72. Cho hình chöõ nhaät ABCD coù AD = m.DC (m > 0). M laø ñieåm treân caïnh AB. Tia phaân giaùc goùc CDM caét BC taïi E. Chöùng minh raèng : DM = AM + m.EC.

73. Cho hình thang ABCD (AB // CD). O laø giao ñieåm cuûa AC vaø BD. Ñöôøng thaúng qua O song song vôùi AB caét AD ôû M. Chöùng minh raèng

a) DOAB ∽ DOCD                                                                                                         b) .

74. Cho a, b, c laø ñoä daøi caùc caïnh cuûa tam giaùc ABC ; x, y, z töông öùng laø ñoä daøi caùc ñöôøng phaân giaùc cuûa goùc ñoái dieän vôùi caùc caïnh ñoù. Chöùng minh raèng :

a) x <                                                                                                                         b) .

75. Cho töù giaùc ABCD coù M, N laàn löôït laø trung ñieåm cuûa caùc ñöôøng cheùo BD, AC (M  N). Ñöôøng thaúng MN caét AD, BC laàn löôït ôû E vaø F. Chöùng minh raèng AE.BF = DE.CF.

76. Cho tam giaùc ABC coù ñöôøng trung tuyeán BM caét ñöôøng phaân giaùc CD ôû N.

Chöùng minh raèng  = 1.

76. Cho tam giaùc ABC caân ñænh A vaø H laø trung ñieåm cuûa caïnh BC. Goïi I laø hình chieáu vuoâng goùc cuûa H leân caïnh AC vaø O laø trung ñieåm cuûa HI. Chöùng minh raèng DBIC ∽ DAOH.

77. Cho tam giaùc ABC vuoâng taïi A coù AH laø ñöôøng cao. Goïi D, E laàn löôït laø hình chieáu cuûa H leân AB, AC.

a) Chöùng minh raèng DAED ∽ DABC.                                                                     b) Cho bieát S_ABC = 2S_ADHE.

Chöùng minh raèng tam giaùc ABC vuoâng caân taïi A.

78. Töø ñieåm M naèm trong tam giaùc ABC laàn löôït veõ caùc ñöôøng thaúng vuoâng goùc vôùi BC, CA, AB taïi D, E, F. Treân caùc tia MD, ME, MF laàn löôït laáy caùc ñieåm A¢, B¢, C¢ sao cho . Chöùng minh raèng M laø troïng taâm cuûa tam giaùc A¢B¢C¢.

CAÙC BAØI TOAÙN CHOÏN LOÏC :

Baøi toaùn 1 : Cho tam giaùc nhoïn ABC coù BD vaø CE laø hai ñöôøng cao caét nhau taïi H. Goïi M laø giao ñieåm cuûa AH vaø BC. Chöùng minh raèng MH.MA = MB.MC.

Nhaän xeùt : Ñeå chöùng minh ñaúng thöùc giöõa caùc ñoaïn thaúng treân ta chöùng minh DMBH ∽ DMAC

Giaûi : DABC coù BD vaø CE laø hai ñöôøng cao caét nhau taïi H. Þ H laø tröïc taâm cuûa tam giaùc ABC

Þ AM ^ BC. Xeùt DMBH () vaø DMAC ()

coù  =  (cuøng phuï vôùi goùc ACB) Þ  DMBH ∽ DMAC (gg)

Þ  Þ MH.MA = MB.MC 

Chuù yù :  Neáu cho BC coá ñònh, A laø ñieåm baát kyø trong maët phaúng chöùa BC

sao cho DABC nhoïn. Khi aáy :

MB.MC = MB( BC – MB) = -(MB² – BC. MB)

              = -(MB² - 2MB + - ) = -(MB - )² +  

Daáu ñaúng thöùc xaûy ra khi : MB = M laø trung ñieåm BC

Töø ñoù ta coù baøi toaùn : " Cho ñoaïn thaúng BC coá ñònh, A laø ñieåm baát kyø trong maët phaúng chöùa BC sao cho tam giaùc ABC nhoïn. Caùc ñöôøng cao AM, BD caét nhau taïi H. Tìm vò trí cuûa M ñeå tích MA. MH ñaït giaù trò lôùn nhaát

·         Neáu ta khoâng chæ döøng taïi ñoù, xeùt baøi toaùn : " Cho DABC nhoïn , ñöôøng cao AM, H laø ñieåm thuoäc ñoaïn AM sao cho : BM. CM = MH.MA. Chöùng minh H laø tröïc taâm DABC "

Ta deã daøng chöùng minh ñöôïc DMBH ∽ DMAC (cgc) Þ  = , maø  (ñoái ñænh)

Do ñoù :  +  =  +  = 90⁰ ( do DMHB vuoâng taïi M) Þ BHAC. Vaäy H laø tröïc taâm DABC.

          Thaät thuù vò vì keát quaû baøi toaùn naøy cho ta giaûi quyeát ñöôïc nhieàu baøi toaùn HAY vaø KHOÙ.

Baøi toaùn : "Cho tam giaùc nhoïn ABC, caùc ñöôøng cao AA¢, BB¢, CC¢ caét nhau taïi H. K laø trung ñieåm cuûa AH. I laø giao ñieåm cuûa B¢C¢ vaø AH. Chöùng minh raèng I laø tröïc taâm cuûa tam giaùc KBC "

Thaäy vaäy :  Þ DA¢KC¢ ∽ DA¢B¢I (g.g)

Þ  Þ A¢I.A¢K = A¢B¢.A¢C¢  (1)

Maø : DA¢BC¢ ∽ DA¢B¢C ( cuøng ñoàng daïng vôùi  DABC )

Þ  Þ A¢B.A¢C = A¢B¢.A¢C¢ (2)

Töø (1), (2) cho : A¢I.A¢K = A¢B.A¢C . Theo keát quaû baøi toaùn treân thì

I laø tröïc taâm cuûa  DKBC.

Baøi toaùn 2 : Giaû söû AC laø ñöôøng cheùo lôùn cuûa hình bình haønh ABCD. Töø ñieåm C haï caùc ñöôøng vuoâng goùc CE vaø CF töông öùng treân ñöôøng keùo daøi cuûa caùc caïnh AB vaø AC.

             Chöùng minh raèng AB.AE + AD.AF = AC².

Nhaän xeùt : Do caùc tam giaùc AEC, ACF vuoâng ñeå xuaát hieän tam giaùc ñoàng daïng,

töø B hay D ta döïng ñöôøng thaúng vuoâng goùc vôùi AC

Giaû söû ta veõ BG ^ AC taïi G. Thaáy ngay : AB.AE = AC.AG

Vaäy : AB.AE + AD.AF = AC²

 AD.AF = AC² - AC.AG = AC(C – AG) = AC. AG.

BC.AF = AC.CG   . Ta caàn chöùng minh : DCBG ∽ DACF

Giaûi : Veõ BG ^ AC taïi G. Ta coù DABG ∽ DACE Þ  

Þ AB.AE = AC.AG              (1)

Maø AF // BC Þ  Þ DCBG ∽ DACF (gg) Þ  Þ BC.AF = AC.CG     (2)

Töø (1) vaø (2) suy ra : AB.AE + AF.BC = AC(AG + CG) = AC².

Vaäy AB.AE + AD.AF = AC².

Vi duï 3 : Cho tam giaùc  ABC, M laø ñieåm thuoäc caïnh BC. Qua M keû

ñöôøng thaúng song song vôùi AC, AB caét AB, AC laàn löôït taïi D vaø E.

Bieát S_BDM = 9cm², S_CME = 16cm². Tính ñieän tích tam giaùc ABC.

Nhaän xeùt : Ta thaáy ngay DBDM ∽ DBAC, maø S_BDM = 9cm² neân ta caàn xaùc ñònh ñöôïc tæ soá ñoàng daïng. Töø DBDM ∽ DMEC vaø dieän tích hai tam giaùc naøy ñeàu bieát neân ta tính ñöôïc tæ soá ñoàng daïng caàn tìm

Giaûi : Xeùt DBDM vaø DMEC coù : (ñoàng vò, ME // AB), (ñoàng vò, MD // AC)

Þ  DBDM ∽ DMEC (gg) Þ  = = Þ  = Þ  = Þ =

Maët khaùc do MD // AC neân DBDM ∽ DBAC Þ  = = Þ S_BAC = . 9 = 47 (cm²)

·         Khoâng döøng ôû ñaây neáu xeùt M laø ñieåm naèm trong tam giaùc, qua M ta keû caùc ñöôøng thaúng

song song vôùi caùc caïnh tam giaùc. Caùc ñöôøng thaúng taïo vôùi caùc caïnh tam giaùc thaønh ba tam giaùc coù dieän tích laàn löôït laø a², b², c² (cm²). Thì khi aáy dieän tích tam giaùc ABC laø laø bao nhieâu?

AÙp duïng baøi toaùn treân coù :

DAHK, MHK  neân S_AHK = ()²

DBEF, MEF  neân S_BEF = ()²

DCDNK, MDN  neân S_CDN = ()²

Suy ra : S_BAC = S_AHK + S_BEF  + S_CDN – 2(S_MHF + S_MDE + S_MNK)

                        = ()² + ()² + ()² – 2(a² + b² +c²)

                        = ()²

Sai laàm : Khi töông töï hoaù vaø khaùi quaùt hoaù laø keát luaän

S_BAC = (a + b + c)². Ta chæ caàn choïn phaûn ví duï thì thaáy ngay keát quaû naøy sai

Vi duï 4 : Cho tam giaùc ABC nhoïn, caùc ñöôøng cao AD, BE, CF caét nhau taïi H

            a)   Chöùng minh raèng H laø giao ñieåm caùc ñöôøng phaân giaùc trong DDEF

            b)  Goïi K laø giao ñieåm cuûa AD vaø EF. Chöùng minh raèng : HK. AD = AK. DH

Nhaän xeùt : Ñeå chöùng minh FC laø phaân giaùc goùc DFE ta chöùng minh  = . Deã daøng nhaän thaáy caû hai goùc naøy ñeàu baèng  thoâng qua hai caëp tam giaùc tam giaùc ñoàng daïng.

Ñaây laø baøi toaùn coù keát quaû quan troïng vaø thöôøng gaëp trong chöông trình lôùp 9.

Giaûi :

a)  Xeùt DAEB vaø DAFC coù : chung, (cuøng phò vôùi )

DAEB ∽ D AFC (gg)  

Xeùt DAEF vaø DABC coù : chung, (cmt)

DAEF ∽ D ABC (cgc)   (1)

Lyù luaän töông töï nhö treâncoù : DBFD ∽ D BCA (cgc)

  (2). Töø (1), (2) cho :  =    FC laø tia phaân giaùc .

Töông töï :  DA laø tia phaân giaùc . Vaäy H laø giao ñieåm caùc ñöôøng phaân giaùc trong tam giaùc ABC

b)  Xeùt DKFD coù : FH laø phaân giaùc trong taïi ñænh H, AFFH FA laø phaân giaùc ngoaøi taïi F cuûa tam giaùc  HK. AD = AK. DH

Chuù yù : Khoâng chæ döøng ôû laïi baøi toaùn treân, ta ñaëc bieät hoaù S_AEF = S_BFD = S_CDE thì :

DAEF ∽ D ABC  =  vaø DDBF ∽ D ABC  = maø: S_AEF = S_BFD

Do ñoù : = =  AE = BDDAEB = DBDA ( caïnh huyeàn, caïnh goùc vuoâng)

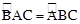. Lyù luaän töông töï ta ñöôïc : . Vaäy : 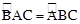=DABCñeàu

Töø ñoù taù coù baøi toaùn : "Cho tam giaùc ABC nhoïn, caùc ñöôøng cao AD, BE, CF caét nhau taïi H bieát S_AEF = S_BFD = S_CDE . Chöùng minh tam giaùc ABC ñeàu"