Đường trung bình
ĐƯỜNG TRUNG BÌNH CỦA TAM GIÁC
 ĐƯỜNG TRUNG BÌNH CỦA HÌNH THANG
ĐƯỜNG TRUNG BÌNH CỦA HÌNH THANG
1) Đường trung bình của tam giác:


 1.1 Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.
1.1 Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.
Định nghĩa: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác
MA = MB và NA = NC
ó MN là đường trung bình rABC
1.2 Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy
MN là đường trung bình rABC =>
MN = BC

 2) Đường trung bình của hình thang:
2) Đường trung bình của hình thang:







 2.1 Đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm cạnh bên thứ hai.
2.1 Đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm cạnh bên thứ hai.
Định nghĩa: Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang.
MA = MD và NB = NC ó MN là đường trung bình của hình thnag ABCD.
2.2 Đường trung bình của hình thang thì song song với hay đáy và bằng nửa tổng hai đáy
MN là đường trung bình của hình thang ABCD
=>
MN =
II. Bài tập cơ bản: SGK
III. Bài tập làm thêm:
1) Cho rABC có G là trọng tâm, H là trực tâm và O là giao điểm của ba đường trung trực. Chứng minh rằng H, G, O thẳng hàng và HG = 2 OG.
2) Cho tam giác ABC có BD, CE là hai trung tuyến. Lấy các điểm M, N trên cạnh BC sao cho BM = MN = NC. Gọi I là giao điểm của AM và BD, K là giao điểm của AN và CE. Chứng minh rằng IK =
3) Cho tam giác ABC (AB < AC). Lấy điểm D thuộc cạnh AB, điểm E thuộc cạnh AC sao cho BD = CE. Gọi M, N, K lần lượt là trung điểm của DE, BC, CD. Chứng minh tam giác MKN cân
4) Cho tam giác ABC, góc A = 80o , trên tia đối của các tia BA, CA lần lượt lấy các điểm P và Q sao cho BP = CQ. Gọi M, N lần lượt là trung điểm BC, PQ. Đường thẳng MN cắt đường thẳng AB và AC tại B' và C'. Tính số đo góc AB'C' ?
5) Cho tam giác ABC có G là trọng tâm. Đường thẳng xy đi qua G và cắt hai cạnh AB , AC. Chứng minh rằng khoảng cách từ A đến đường thẳng xy bằng tổng các khoảng cách từ B và C đến đường thẳng xy.
6) Cho tam giác ABC có hai trung tuyến AD và CE. Trên tia đối của tia BA lấy điểm K sao cho BK = BE. Trên tia đối của tia CB lấy điểm H sao cho CH = CD. Gọi M là giao điểm của AC và EH. Chứng minh rằng:
a) M là trung điểm EH
b) Ba điểm K, D, M thẳng hàng
Tags: THCS Nguyễn Du, Toán Lớp 8, Toán THCS


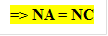








 Trang Trước
Trang Trước







No comments: