ĐỀ CƯƠNG ÔN TẬP HỌC KÌ II_ TOÁN 9
ÑEÀ CÖÔNG OÂN TAÄP HOÏC KÌ II_ TOAÙN 9
ÑAÏI SOÁ
A HỆPHÖÔNG TRÌNH BAÄC NHAÁT HAI AÅN
1/. Phöông trình baäc nhaát hai aån soá :
*Nghieäm cuûa phöông trình:
+ Caùc caùch giaûi: Ñoà thò,phöông phaùp theá, phöông phaùp coäng.
a < 0: Haøm soá ñoàng bieán khi x < 0 vaø nghòch bieán khi x > 0.
b)Đoà thò :Ñoà thò haøm soá y = ax2( a ¹ 0) laø parabol coù ñaëc ñieåm :
y = ax2 vôùi a > 0 y = ax2 vôùi a < 0
 |
 | ||
C PHÖÔNG TRÌNH BAÄC HAI MỘT ẨN
1 Ñònh nghóa : Phöông trình baäc hai moät aån soá laø phöông trình coù daïng ax2 + bx + c = 0 (a 0;a,b,c
0;a,b,c  R; aån x)
R; aån x)
 0;a,b,c
0;a,b,c  R; aån x)
R; aån x)
Coâng thöùc nghieäm toång quaùt
|
Coâng thöùc nghieäm thu goïn
|
4/. Ñònh lyù Vi-eùt: Neáu phöông trình baäc hai ax2 + bx + c = 0 (a 0) coù 2 nghieäm x1,x2 thì toång vaø tích cuûa 2 nghieäm ñoù laø: S = x1+ x2 =
0) coù 2 nghieäm x1,x2 thì toång vaø tích cuûa 2 nghieäm ñoù laø: S = x1+ x2 =  vaø P = x1.x2 =
vaø P = x1.x2 = 
 0) coù 2 nghieäm x1,x2 thì toång vaø tích cuûa 2 nghieäm ñoù laø: S = x1+ x2 =
0) coù 2 nghieäm x1,x2 thì toång vaø tích cuûa 2 nghieäm ñoù laø: S = x1+ x2 =  vaø P = x1.x2 =
vaø P = x1.x2 = 
+ a vaø c traùi daáu (a.c < 0) thì phöông trình coù 2 nghieäm phaân bieät.
6/. Toång vaø tích:Neáu hai soá x1,x2 thoûa x1+ x2 = S ; x1.x2 = P vaø S2 – 4P 0 thì x1,x2 laø nghieäm cuûa pt x2 – Sx + P = 0
0 thì x1,x2 laø nghieäm cuûa pt x2 – Sx + P = 0
 0 thì x1,x2 laø nghieäm cuûa pt x2 – Sx + P = 0
0 thì x1,x2 laø nghieäm cuûa pt x2 – Sx + P = 0
7/Töông giao cuûa Parabol vaø ñöôøng thaúng
Phöông phaùp: (P) : y = ax2 (D) : y = bx + c
Phöông trình hoaønh ñoä giao ñieåm cuûa (D) vaø (P): ax2= bx + c (1)
(1) voâ nghieäm Û (D) Khoâng caét (P) Û D < 0
(1) coù nghieäm keùp Û (D) tieáp xuùc (P) Û D = 0
(1) coù 2nghieäm phaân bieät Û (D) caét (P) Û D > 0
(P) (P) (P)
(D)
(D)
(D)
O x O x o
B)HÌNH HOÏC
I) Góc trong đường tròn: Các loại góc trong đường tròn
a)Góc ở tâm: Soá ño cuûa goùc ôû taâm baèng soá ño cuûa cung bò chaén.
b)Góc nội tiếp:
- Soá ño cuûa goùc noäi tieáp baèng nöûa soá ño cung bò chaén.
-
Caùc goùc noäi tieáp baèng nhau chaén caùc cung baèng nhau.
-
Caùc goùc noäi tieáp cuøng chaén moät cung hoaëc chaén caùc cung baèng nhau thì baèng nhau.
- Goùc noäi tieáp ≤ 900 coù soá ño baèng nöûa soá ño cuûa goùc ôû taâm cuøng chaén moät cung.
-
Goùc noäi tieáp chaén nöûa ñöôøng troøn laø goùc vuoâng.
c) Góc tạo bởi tia tiếp tuyến và dây cung:
-
Soá ño cuûa goùc taïo bôûi tia tieáp tuyeán vaø daây cung baèng nöûa soá ño cuûa cung bò chaén.
-
Goùc taïo bôûi tia tieáp tuyeán vaø daây cung vaø goùc noäi tieáp cuøng chaén noät cung thì baèng nhau.
d) Góc có đỉnh ở bên trong hay bên ngoài đường tròn
-
Soá ño cuûa goùc coù ñænh ôû beân trong ñöôøng troøn baèng nöûa toång soá ño hai cung bò chaén
-
Soá ño cuûa goùc coù ñænh ôû beân ngoaøi ñöôøng troøn baèng nöûa hieäu soá ño hai cung bò chaén.
II) Lieân hệ giữa cung và dây cung:
* Định lí 1: Đối với hai cung nhỏ trong một đường tròn:
a) Hai cung bằng nhau căng hai dây bằng nhau b) Hai dây bằng nhau căng hai cung bằng nhau.
* Định lí 2: Đối với hai cung nhỏ trong một đường tròn:
a) Cung lớn hơn căng dây lớn hơn b) Dây lớn hơn căng cung lớn hơn.
*Định lí 3:
a)Ñöôøng kính ^ vôùi daây thì qua trung ñieåm cuûa daây &qua ñieåm chính giöõa cuûa cung caêng daây ñoù
b) Ñöôøng kính qua ñieåm chính giöõa cuûa cung thì vôùi ^daây caêng cung ñoùtaïi trung ñieåm
c) Ñöôøng kính qua trung ñieåm daây khoâng qua taâm thì ^ vôùi daây vaø qua ñieåm chính giöõa cuûa cung caêng daây ñoù
III) Tứ giác nội tiếp:
a) Định nghĩa:Tứ giác nội tiếp một đường tròn là tứ giác có bốn đỉnh nằm trên một đường tròn .
Đường tròn đó được gọi là đường tròn ngoại tiếp tứ giác.
b) Daáu hieäu nhaän bieát :
* Tứ giác có bốn đỉnh cùng thuộc một đường tròn
* Tứ giác có tổng hai góc đối diện bằng 1800
* Tứ giác coù goùc ngoaøi taïi moät ñænh baèng goùc trong ôû ñænh ñoái dieän
*Tứ giác có hai đỉnh kề nhìn cạnh đối diện dưới caùc góc bằng nhau
*Hình chữ nhật ,hình vuông ,hình thang cân là tứ giác nội tiếp
IV)Caùc coâng thöùc
B/Baøi taäp :
A HẼPHÖÔNG TRÌNH BAÄC NHAÁT HAI AÅN
1)Vôùi giaù trò naøo cuûa a vaø b thì heä phöông trình sau töông ñöông :
2)Giaûi heä phöông trình
B PHÖÔNG TRÌNH BAÄC HAI
I Giaûi phöông trình:
II Giaûi phöông trình qui veà phöông trình baäc hai:
III Ñònh tham soá ñeå phöông trình baäc hai thoaû ñieàu kieän veà nghieäm soá:
1/ Ñònh m ñeå phöông trình coù hai nghieäm soá phaân bieät
2/ Ñònh m ñeå phöông trình coù nghieäm soá keùp;Tính n s keùp :
3/ Ñònh m ñeå phöông trình voâ nghieäm :
C HEÄTHÖÙC VIEØET
1/Nhaåm nghieäm:
2/Aùp duïng heä thöùc Vi et
a) Ñònh m ñeå phöông trình coù 2 nghieäm phaân bieät
c) Tìm heä thöùc lieân heä giöõa caùc nghieäm soá khoâng thuoäc vaøo m
5/ Cho phöông trình (m+2)x2 – 2(m -1)x + 3 -m = 0
b) Ñònh m ñeå phöông trình coù 2 nghieäm soá thoûa
c) Laäp 1 heä thöùc giöõa x1 vaø x2 khoâng phuï thuoäc vaøo m
d) Laäp phöông trình baäc 2 coù 2 nghieäm soá
6/ Cho phöông trình (m +2)x2 – (2m-1)x –3+ m = 0
a) Chöùng minh phöông trình coù nghieäm "m
b) Tìm m ñeå phöông trình coù 2 nghieäm phaân bieät x1 ,x2 trong ñoù nghieäm naøy gaáp 2 laàn nghieäm kia.
D/HAØM SOÁ_ÑOÀ THÒ HAØM SOÁ
a) Veõ (P)
b) Tìm toïa ñoä giao ñieåm cuûa (P) vaø (D):y = -x -4 baèng ñoà thò vaø pheùp toaùn
c) Vieát phöông trình ñöôøng thaúng (D') // (D) vaø tieáp xuùc vôùi (P). Xaùc ñònh toïa ñoä tieáp ñieåm M
a) Veõ (P)
b) Tìm toïa ñoä giao ñieåm cuûa (P) vaø (D):y = x -1 baèng ñoà thò vaø pheùp toaùn
c) Vieát phöông trình ñöôøng thaúng (D') // (D) vaø (D') caét (P) taïi ñieåm M coù hoaønh ñoä -1
a) Veõ (P)
c) Vieát phöông trình ñöôøng thaúng (D') ^ (D) vaø tieáp xuùc vôùi (P). Xaùc ñònh toïa ñoä tieáp ñieåm M
E GIAÛI BAØI TOAÙN BAÈNG CAÙCH LAÄP PHÖÔNG TRÌNH
1/Moät tam giaùc vuoâng coù hieäu hai caïnh goùc vuoâng laø 14cm dieän tích laø 120 cm2 Tính caùc caïnh goùc vuoâng
2/Moät hình chöõ nhaät coù chu vi 28m vaø ñöôøng cheùo coù ñoä daøi laø 10 m Tính kích thöôùc hình chöõ nhaät
3/ Moät caâu laïc boä coù 320 choã ngoài nhöng trong moät buoåi sinh hoaït coù tôùi 420 ngöôøi ñeán döï neân phaûi ñaët theâm moät daõy gheá vaø moãi daõy theâm 4 gheá Hoûi luùc ñaàu caâu laïc boä coù maáy daõy gheá . Bieát soá daõy gheá lôùn hôn 10
4/ Moät maûnh ñaát hình chöõ nhaät coù chu vi 18m vaø dieän tích 20m2.Tính chieàu daøi,roäng cuûa maûnh ñaát.
ÑEÀ THI HOÏC KYØ II Naêm Hoïc 2007_2008
Baøi 1: Giải phương trình vaø heä phương trình :
Baøi 2: Cho phöông trình x2 + (2m -1)x - 2m = 0
a) Chöùng minh phöông trình coù nghieäm vôùi moïi m Î R.
b) Baèng pheùp toùan haõy tìm toïa ñoä giao ñieåm cuûa 2 ñoà thò treân
Baøi 4: Cho  caân taïi A coù caïnh ñaùy nhoû hôn caïnh beân , noäi tieáp ñöôøng troøn (O;R),Tieáp tuyeán taïi B vaø C cuûa ñöôøng troøn laàn löôït caét tia AC vaø tia AB ôû D vaø E
caân taïi A coù caïnh ñaùy nhoû hôn caïnh beân , noäi tieáp ñöôøng troøn (O;R),Tieáp tuyeán taïi B vaø C cuûa ñöôøng troøn laàn löôït caét tia AC vaø tia AB ôû D vaø E
 caân taïi A coù caïnh ñaùy nhoû hôn caïnh beân , noäi tieáp ñöôøng troøn (O;R),Tieáp tuyeán taïi B vaø C cuûa ñöôøng troøn laàn löôït caét tia AC vaø tia AB ôû D vaø E
caân taïi A coù caïnh ñaùy nhoû hôn caïnh beân , noäi tieáp ñöôøng troøn (O;R),Tieáp tuyeán taïi B vaø C cuûa ñöôøng troøn laàn löôït caét tia AC vaø tia AB ôû D vaø E
ÑEÀ THI HOÏC KYØ II Naêm Hoïc 2008_2009
Baøi 1: Giải phương trình vaø heä phương trình :
Baøi 2: Cho phöông trình x2 + 2m x – 2m2 = 0
a) Chöùng minh phöông trình coù nghieäm vôùi moïi m Î R.
b)Tính toång vaø tích cuûa hai nghieäm theo m
c) Goïi x1, x2 laø hai nghieäm cuûa phöông trình.Tìm m ñeå x1+ x2= x1. x2
a)Veõ ñoà thò cuûa haøm soá treân b)Tìm caùc ñieåm thuoäc ñoà thò (P) coù tung ñoä laø -5
Baøi 4 : Cho tam giaùc ABC nhoïn Caùc ñöôøng cao AD , BE , CF caét nhau taïi H.
a)Chöùng minh :Caùc töù giaùc BCEF ,AEHF laø caùc töù giaùc noäi tieáp
b) Chöùng minh :EH.EB = EA.EC
ÑEÀ THI HOÏC KYØ II Naêm Hoïc 2009_2010
Baøi 1: Giải phương trình vaø heä phương trình :
a) Chöùng minh phöông trình trên luôn luôn coù nghieäm vôùi moïi m Î R.
b)Tính toång vaø tích cuûa hai nghieäm theo m
a)Veõ ñoà thò cuûa haøm soá treân
b)Tìm caùc ñieåm M thuoäc ñoà thò (P) sao cho M coù hoành độ bằng với tung ñoä
Baøi 4 :Cho ñöôøng troøn tâm O ,đường kính AB = 8.Gọi Ax,By lần lượt là các tiếp tuyến tại A và B của ñöôøng troøn (O).Qua điểm M thuộc (O) vẽ tiếp tuyến thứ ba của ñöôøng troøn (O) ( M là tiếp điểm , M khác A và B ) Tiếp tuyến này cắt Ax tại C ,cắt By tại D.( AC > BD )
a)Chöùng minh :Caùc töù giaùc OACM ,OBDM laø caùc töù giaùc noäi tieáp
b)OC cắt AM tại E ; OD cắt BM tại F .Tứ giác OEMF là hình gì ?
c)Gọi I là trung điểm của OC và K là trung điểm của OD.Chứng minh tứ giác OIMK là tứ giác nội tiếp
d)Cho AC +BD =10 Tính diện tích tứ giác OIMK
Subscribe to:
Post Comments (Atom)





































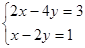



























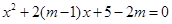





























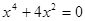




 Trang Trước
Trang Trước



No comments: