Câu Hình Đề 1 - Lê Lợi
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn (O;R). Kẻ đường cao AD của tam giác ABC, đướng kính AM của (O). đường cao AD cắt (O) tại điểm thứ 2 K.
a. Gọi H là điểm đối xứng của K qua BC, CH cắt AB tại F. chứng minh: H là trực tâm của tam giác ABC.
b. BH cắt AC tại E. Chứng minh trung điểm I của AH thuộc đường tròn ngoại tiếp tam giác DEF.
c. AH cắt EF tại P, AM cắt BC tại Q. chứng minh:PQ//MH.
d. Qua P kẻ đường thẳng song song với BC cắt AB tại T và cắt BE tại N. Chứng minh: P là trung điểm của đoạn thảng NT.
Giải:
a. Chứng minh H là trực tâp của tam giác ABC:
Tam giác CHK có:
ü CD là đường cao
ü CD là đường trung tuyến (do D là trung điểm của HK)
ð CHK là tam giác cân tại C (có đường cao vừ là đường trung tuyến)
ð CD cũng là đường phân giác của tam giác CHK
Mà  (góc nội tiếp cùng chắn cung BK)
(góc nội tiếp cùng chắn cung BK)
Trong tam giác CHD có:
Thay (1),(2) vào (*) ta được:
Suy ra tam giác AHF vuông tại F
=> CF là đường cao của tam giác ABC
Vậy H là trực tâm của tam giác ABC(vì H là giao điểm của 2 đường cao CF và AD)
b. Chứng minh IDFE nội tiếp.
v Tam giác AEH có:
ü Vuông tại E
ü EI là đường trung tuyến
=>IA=IE=IH (tính chất đường trung tuyến trong tam giác vuông)
=>AEI là tam giác cân tại I
Chứng minh tương tự ta có:
Tứ giác DEIF ta xét tổng sau:
Thay (@),(@@) vào biểu thức trên ta được:
Lại có:
Thay vào (I) ta được:
(do tam giác ADC vuông tại D)
Vậy EIFD nội tiếp được đường tròn (có tổng 2 góc đối bằng 180)
=>I thuộc đường tròn ngoại tiếp DEF.
c. Chứng minh PQ//MH
Tam giác FPD có FH là đường phân giác (cách chứng minh phân giác giống như làm ở câu b)
Lại có: FH FA (do CF là đường cao)
FA (do CF là đường cao)
Nên: FA là phân giác ngoài của tam giác FPD
Kết hợp 2 ý trên ta có:
Mà: HD=DK nên ta có:
Tam giác AKM có:
ü MK AK ( do góc MKA là góc nội tiếp chắn nữa đường tròn)
AK ( do góc MKA là góc nội tiếp chắn nữa đường tròn)
=>DQ//MK
Theo Talet ta có:
Vậy PQ//MH (theo Talet - ở đây xét tính chất Talet trong tam giác AHM)
d. Chứng minh P là trung điểm của NT
Tứ giác APNE có:
ü PN//BC
Do đó, ta có:
ü  (do BE là đường cao của tam giác ABC)
(do BE là đường cao của tam giác ABC)
=>APNE nội tiếp. (có 2 góc cùng nhìn cạnh AN bằng nhau)
=> (góc nội tiếp cùng chắn cung AP)
(góc nội tiếp cùng chắn cung AP)
Mà  (góc trong và góc ngoài đối diện của tứ giác nội tiếp BCEF)
(góc trong và góc ngoài đối diện của tứ giác nội tiếp BCEF)
Vậy tam giác ANT cân tại A (có 2 góc đáy bằng nhau)
Với lại: AP là đường cao của tam giác ANT (do PN  AK)
AK)
Suy ra: AP củng là đường trung tuyến của tam giác ANT (tính chất tma giác cân)
Do đó: PN=PT
Kết luận: P là trung điểm của NT.






















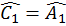

















 Trang Trước
Trang Trước



No comments: