Toán hình 9 - Ôn Thi Vào Lớp 10 - Bài 14
Bài 14 Cho đường tròn (O; R) , đường kính AB . Trên tiếp tuyến kẻ từ A của đường tròn này lấy điểm C sao cho AC = AB . Từ C kẻ tiếp tuyến thứ hai CD của đường tròn (O; R), với D là tiếp điểm.
a) Chứng minh rằng ACDO là một tứ giác nội tiếp.
b) Gọi H là giao điểm của AD và OC. Tính theo R độ dài các đoạn thẳng AH; AD.
c) Đường thẳng BC cắt đường tròn (O; R) tại điểm thứ hai M. Chứng minh  .
.
 d) Đường tròn (I) ngoại tiếp tam giác MHB. Tính diện tích phần của hình tròn này nằm ngoài đường tròn (O; R).
d) Đường tròn (I) ngoại tiếp tam giác MHB. Tính diện tích phần của hình tròn này nằm ngoài đường tròn (O; R).
BÀI GIẢI
a) Chứng minh tứ giác ACDO nội tiếp:
nội tiếp được trong một đường tròn.
b) Tính theo R độ dài các đoạn thẳng AH; AD:
CA = CD (tính chất hai tiếp tuyến cắt nhau);
nên  =
=  =
=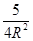 . Vậy AH =
. Vậy AH =  và AD = 2AH =
và AD = 2AH =  .
.
 (góc nội tiếp chắn nửa đường tròn)
(góc nội tiếp chắn nửa đường tròn)  .
.
Hai đỉnh H và M cùng nhìn AC dưới góc 900 nên ACMH là tứ giác nội tiếp.
Tam giác ACB vuông tại A, AC = AB(gt) nên vuông cân. Vậy  .
.
d) Tính diện tích hình tròn (I) nằm ngoài đường tròn (O) theo R:
Từ  và
và 
 mà
mà  (do
(do  CAB vuông cân ở B).
CAB vuông cân ở B).
Do đó  . Vậy tâm I đường tròn ngoại tiếp tam giác MHB là trung điểm MB.
. Vậy tâm I đường tròn ngoại tiếp tam giác MHB là trung điểm MB.
Gọi S là diện tích phần hình tròn (I) ở ngoài đường tròn (O).S1 là diện tích nửa hình tròn đường kính MB. S2 là diện tích viên phân MDB.
Ta có S = S1 – S2 . Tính S1:
Tags: Các bài Toán Hình Ôn Thi Vào Lớp 10














 Trang Trước
Trang Trước



No comments: