Toán hình 9 - Ôn Thi Vào Lớp 10 - Bài 13
Bài 13 Cho đường tròn (O;R) có đường kính AB. Trên đường tròn (O;R) lấy điểm M sao cho  . Vẽ đường tròn (B; BM) cắt đường tròn (O; R) tại điểm thứ hai là N.
. Vẽ đường tròn (B; BM) cắt đường tròn (O; R) tại điểm thứ hai là N.
a) Chứng minh AM và AN là các tiếp tuyến của đường tròn (B; BM).
b) Kẻ các đường kính MOI của đường tròn (O; R) và MBJ của đường tròn (B; BM). Chứng minh N, I và J thẳng hàng và JI . JN = 6R2
 c) Tính phần diện tích của hình tròn (B; BM) nằm bên ngoài đường tròn (O; R) theo R.
c) Tính phần diện tích của hình tròn (B; BM) nằm bên ngoài đường tròn (O; R) theo R.
BÀI GIẢI
a) Chứng minh AM và AN là các tiếp tuyến của
(góc nội tiếp chắn nửa đường tròn(O)).
Điểm M và N thuộc (B;BM); AM  MB
MB
và AN  NB. Nên AM; AN là các tiếp tuyến của (B; BM).
NB. Nên AM; AN là các tiếp tuyến của (B; BM).
b) Chứng minh N; I; J thẳng hàng và JI .JN = 6R2.
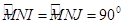 (các góc nội tiếp chắn nửa đường tròn tâm O và tâm B).
(các góc nội tiếp chắn nửa đường tròn tâm O và tâm B).
Nên IN MN và JN
MN và JN  MN . Vậy ba điểm N; I và J thẳng hàng.
MN . Vậy ba điểm N; I và J thẳng hàng.
Tam giác MJI có BO là đường trung bình nên IJ = 2BO = 2R.
Tam giác AMO cân ở O (vì OM = OA),  nên tam giác MAO đều.
nên tam giác MAO đều.
AB  MN tại H (tính chất dây chung của hai đường tròn (O) và (B) cắt nhau).
MN tại H (tính chất dây chung của hai đường tròn (O) và (B) cắt nhau).
Nên OH = 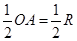 . Vậy HB = HO + OB =
. Vậy HB = HO + OB = 

 .
.
Vậy JI . JN = 2R . 3R = 6R2
c) Tính diện tích phần hình tròn (B; BM) nằm ngoài đường tròn (O; R) theo R:
Gọi S là diện tích phần hình tròn nằm (B; BM) nằm bên ngoài hình tròn (O; R). S1 là diện tích hình tròn tâm (B; BM). S2 là diện tích hình quạt MBN. S3 ; S4 là diện tích hai viên phân cung MB và NB của đường tròn (O; R).
Ta có : S = S1 – (S2 + S3 + S4).
Tính S3: S3 = Squạt MOB – SMOB. 
 Squạt MOB =
Squạt MOB =  .
.
Tags: Các bài Toán Hình Ôn Thi Vào Lớp 10

















 Trang Trước
Trang Trước





No comments: