Bài 6 Cho tam giác ABC có ba góc nhọn. Đường tròn đường kính BC cắt cạnh AB, AC lần lượt tại E và F ; BF cắt EC tại H. Tia AH cắt đường thẳng           BC tại N.

a) Chứng minh tứ giác HFCN nội tiếp.

b) Chứng minh FB là phân giác của .

c) Giả sử AH = BC . Tính số đo góc  của DABC.

BÀI GIẢI CHI TIẾT                                                                                          

a) Chứng minh tứ giác HFCN nội tiếp:

Ta có :

(góc nội tiếp chắn nửa đường tròn đường kính BC)

Tứ giác HFCN có nên nội tiếp được trong

đường tròn đường kính HC) (đpcm).

b) Chứng minh FB là tia phân giác của góc EFN:                                 

Ta có (hai góc nội tiếp cùng chắn  của đường tròn đường kính BC).

(hai góc nội tiếp cùng chắn  của đường tròn đường kính HC).

Suy ra: 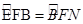. Vậy FB là tia phân giác của góc EFN (đpcm)

c) Giả sử AH = BC. Tính số đo góc BAC của tam giác ABC:

FAH và FBC có: , AH = BC (gt), (cùng phụ ).

Vậy FAH = FBC (cạnh huyền- góc nhọn).

Suy ra: FA = FB.

AFB vuông tại F; FA = FB nên vuông cân. Do đó .