Bài 4 Cho nửa đường tròn tâm O đường kính AB. Từ điểm M trên tiếp tuyến Ax của nửa đường tròn vẽ tiếp tuyến thứ hai MC (C là tiếp điểm). Hạ CH vuông góc với AB, đường thẳng MB cắt  nửa đường tròn (O) tại Q và cắt CH tại N. Gọi giao điểm của MO và AC là I. Chứng minh rằng:

a) Tứ giác AMQI nội tiếp.  b) .  c) CN = NH.

(Trích đề thi tuyển sinh vào lớp 10 năm học 2009-2010 của sở GD&ĐT Tỉnh Bắc Ninh)

BÀI GIẢI CHI TIẾT

a) Chứng minh tứ giác AMQI nội tiếp:

Ta có: MA = MC (tính chất hai tếp tuyến cắt nhau)

OA = OC (bán kính đường tròn (O))

Do đó: MO  AC .

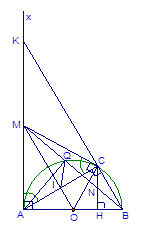
(góc nội tiếp chắn nửa đường tròn (O))

. Hai đỉnh I và Q cùng nhìn AM dưới                            Hình 5

một góc vuông nên tứ giác AMQI nội tiếp được

trong một đường tròn. 

b) Chứng minh:.

Tứ giác AMQI nội tiếp nên           Hình 6                                   

(cùng phụ ) (2).

có OA = OC nên cân ở O.   (3). Từ (1), (2) và (3) suy ra .

c) Chứng minh CN = NH.

Gọi K là giao điểm của BC và tia Ax. Ta có: (góc nội tiếp chắn nửa đường tròn(O)).

AC  BK , AC  OM  OM // BK.

Tam giác ABK có: OA = OB, OM // BK MA = MK.

Áp dụng hệ quả định lí Ta let cho có NH // AM (cùng AB) ta được:

(4). Áp dụng hệ quả định lí Ta let cho có CN // KM (cùng AB) ta được:   (5).

Từ (4) và (5) suy ra: . Mà KM = AM nên CN = NH (đpcm).