Toán Hình - Ôn Thi Vào Lớp 10 - bài 3
Bài 3 Cho nửa đường tròn (O) đường kính AB = a. Gọi Ax, By là các tia vuông góc với AB ( Ax, By thuộc cùng một nửa mặt phẳng bờ AB). Qua điểm M thuộc nửa đường tròn (O) (M khác A và B) kẻ tiếp tuyến với nửa đường tròn (O); nó cắt Ax, By lần lượt ở E và F.
2. Chứng minh tứ giác AEMO nội tiếp; hai tam giác MAB và OEF đồng dạng.
 3. Gọi K là giao điểm của AF và BE, chứng minh
3. Gọi K là giao điểm của AF và BE, chứng minh  .
.
4. Khi MB =  .MA, tính diện tích tam giác KAB theo a.
.MA, tính diện tích tam giác KAB theo a.
BÀI GIẢI CHI TIẾT
EA, EM là hai tiếp tuyến của đường tròn (O)
cắt nhau ở E nên OE là phân giác của  .
.
Tương tự: OF là phân giác của  .
.
Mà  và
và  kề bù nên:
kề bù nên:  (đpcm) hình 4
(đpcm) hình 4
2. Chứng minh: Tứ giác AEMO nội tiếp; hai tam giác MAB và OEF đồng dạng.
Tứ giác AEMO có  nên nội tiếp được trong một đường tròn.
nên nội tiếp được trong một đường tròn.
 Tam giác AMB và tam giác EOF có:
Tam giác AMB và tam giác EOF có: ,
,  (cùng chắn cung MO của đường tròn ngoại tiếp tứ giác AEMO. Vậy Tam giác AMB và tam giác EOF đồng dạng (g.g).
(cùng chắn cung MO của đường tròn ngoại tiếp tứ giác AEMO. Vậy Tam giác AMB và tam giác EOF đồng dạng (g.g).
3. Gọi K là giao điểm của AF và BE, chứng minh  .
.
Tam giác AEK có AE // FB nên:  . Mà : AE = ME và BF = MF (t/chất hai tiếp tuyến cắt nhau). Nên
. Mà : AE = ME và BF = MF (t/chất hai tiếp tuyến cắt nhau). Nên  . Do đó MK // AE (định lí đảo của định lí Ta- let). Lại có: AE
. Do đó MK // AE (định lí đảo của định lí Ta- let). Lại có: AE  AB (gt) nên MK
AB (gt) nên MK  AB.
AB.
4. Khi MB =  .MA, tính diện tích tam giác KAB theo a.
.MA, tính diện tích tam giác KAB theo a.
Gọi N là giao điểm của MK và AB, suy ra MN  AB.
AB.
 FEA có MK//AE nên
FEA có MK//AE nên  (1).
(1).  BEA có NK//AE nên
BEA có NK//AE nên  (2).
(2).
Từ (1), (2) và (3) suy ra  . Vậy MK = NK.
. Vậy MK = NK.
Tam giác AKB và tam giác AMB có chung đáy AB nên:  .
.







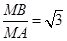






 Trang Trước
Trang Trước



No comments: