Toán Hình 9 - Ôn Thi Vào Lớp 10 - Bài 5
Bài 5 Cho đường tròn tâm O đường kính AB có bán kính R, tiếp tuyến Ax. Trên tiếp tuyến Ax lấy điểm F sao cho BF cắt đường tròn tại C, tia phân giác của góc ABF cắt Ax tại E và cắt đường tròn tại D.
a) Chứng minh OD // BC.
b) Chứng minh hệ thức: BD.BE = BC.BF
c) Chứng minh tứ giác CDEF nội tiếp.
d) Xác định số đo của góc ABC để tứ giác AOCD là hình thoi. Tính diện tích hình thoi AOCD theo R.
a) Chứng minh OD // BC. Hình 7
Mà  (gt) nên
(gt) nên  . Do đó: OD // BC.
. Do đó: OD // BC.
b) Chứng minh hệ thức: BD.BE = BC.BF.
 (góc nội tiếp chắn nửa đường tròn (O)
(góc nội tiếp chắn nửa đường tròn (O)  .
.
 (góc nội tiếp chắn nửa đường tròn (O)
(góc nội tiếp chắn nửa đường tròn (O)  .
.
 vuông ở A (do Ax là tiếp tuyến ), có AD
vuông ở A (do Ax là tiếp tuyến ), có AD  BE nên:
BE nên:
AB2 = BD.BE (1).
 vuông ở A (do Ax là tiếp tuyến), có AC
vuông ở A (do Ax là tiếp tuyến), có AC  BF nên AB2 = BC.BF (2).
BF nên AB2 = BC.BF (2).
Từ (1) và (2) suy ra: BD.BE = BC.BF.
c) Chứng minh tứ giác CDEF nội tiếp:
Ta có:
 (hai góc nội tiếp cùng chắn cung BC)
(hai góc nội tiếp cùng chắn cung BC)
Do đó tứ giác CDEF nội tiếp.
Cách khác


 và
và  có:
có:  chung và
chung và  (suy từ BD.BE = BC.BF) nên chúng đồng dạng (c.g.c).
(suy từ BD.BE = BC.BF) nên chúng đồng dạng (c.g.c).
Suy ra:  . Vậy tứ giác CDEF là tứ giác nội tiếp.
. Vậy tứ giác CDEF là tứ giác nội tiếp.
d) Xác định số đo của góc ABC để tứ giác AOCD là hình thoi:
Ta có:  (do BD là phân giác
(do BD là phân giác  )
)  .
.
Tứ giác AOCD là hình thoi  OA = AD = DC = OC
OA = AD = DC = OC
Vậy  thì tứ giác AOCD là hình thoi.
thì tứ giác AOCD là hình thoi.
Tính diện tích hình thoi AOCD theo R:
Tags: Các bài Toán Hình Ôn Thi Vào Lớp 10


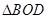
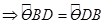







 Trang Trước
Trang Trước





No comments: