KIỂM TRA HỌC KỲ I TOÁN- KHỐI 10 TRƯỜNG THPT GIỒNG ÔNG TỐ
SỞ GIÁO DỤC VÀ ĐÀO TẠO TP HỒ CHÍ MINH TRƯỜNG THPT GIỒNG ÔNG TỐ | KIỂM TRA HỌC KỲ I NĂM HỌC 2019-2020 Môn: TOÁN- KHỐI 10 Thời gian làm bài: 90 phút, không kể thời gian phát đề |
ĐỀ CHÍNH THỨC (gồm có 01 trang) |
Họ tên thí sinh: Lớp: Số báo danh: |
Câu 1. (1 điểm) Cho hàm số có đồ thị là
có đồ thị là . Tìm phương trình của
. Tìm phương trình của  biết
biết  đi qua A(2; 0) và có trục đối xứng
đi qua A(2; 0) và có trục đối xứng  .
.
Câu 2. (2 điểm) Giải các phương trình sau:
2)
Câu 3. (1 điểm) Giải hệ phương trình: 
Câu 4. (1 điểm) Cho phương trình:  (
(  là tham số).
là tham số).
Tìm m để phương trình có hai nghiệm phân biệt  thỏa
thỏa  .
.
Câu 5. (1 điểm) Tìm giá trị nhỏ nhất của hàm số  ,với
,với 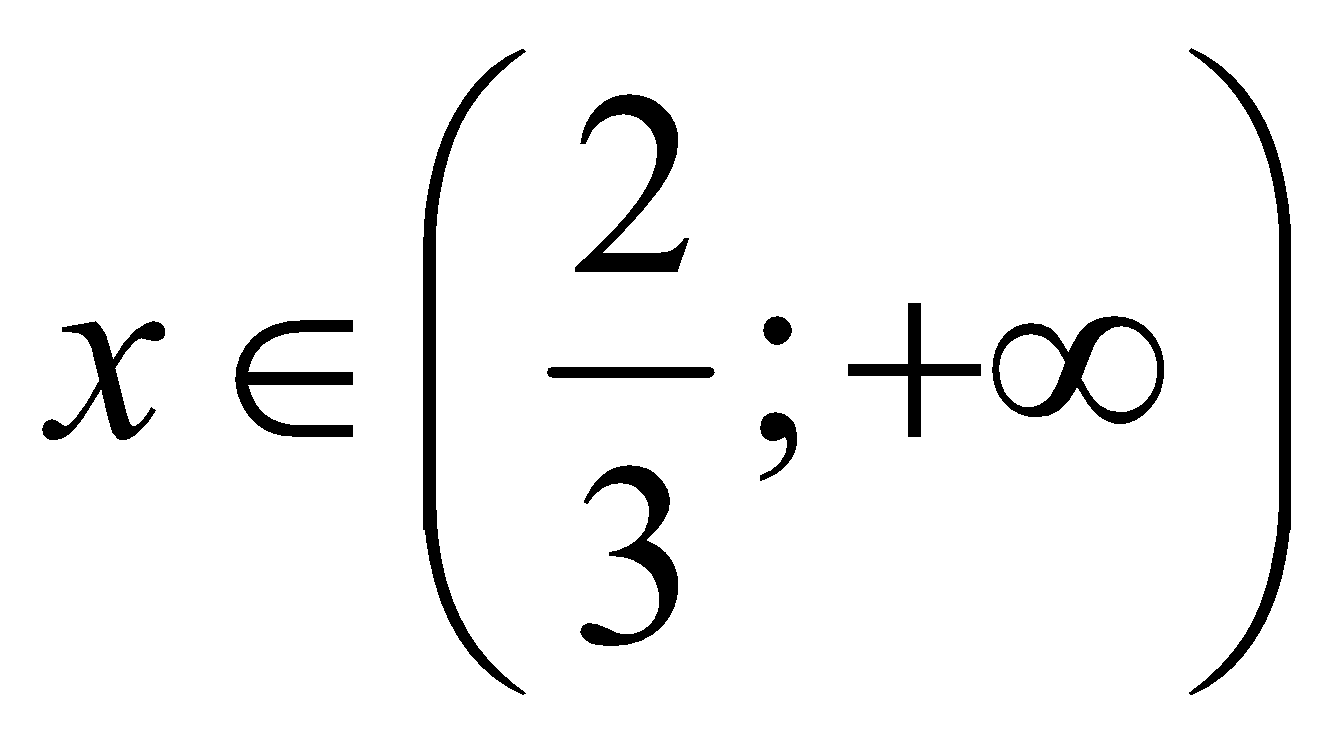 .
.
Câu 6. (2 điểm)
1) Cho hình vuông ABCD có AB = a. Tính theo a các tích vô hướng  .
.
2) Cho tam giác ABC có 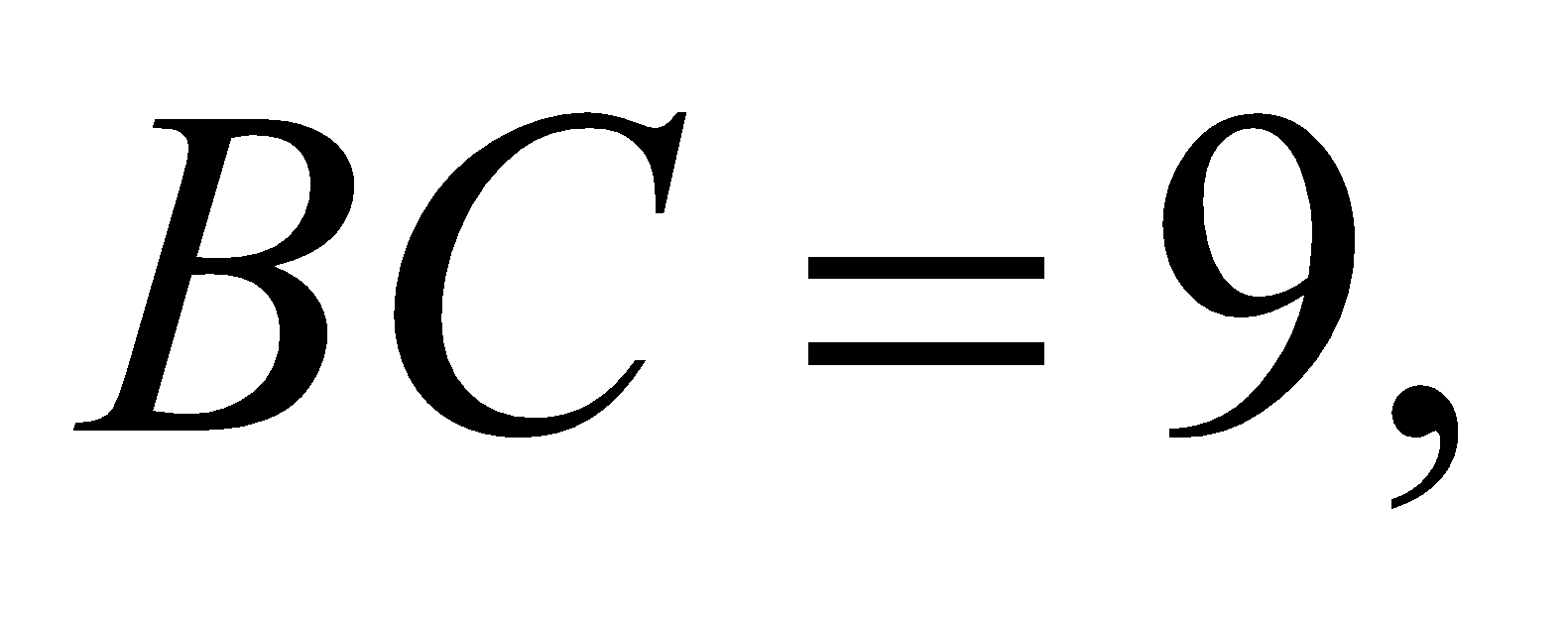
 và
và  Tính bán kính đường tròn nội tiếp tam giác ABC.
Tính bán kính đường tròn nội tiếp tam giác ABC.
Câu 7. (2 điểm) Trong mặt phẳng tọa độ Oxy, cho tam giác ABC biết A(1;4),
B(-2; -1), C(3;1).
Tính chu vi tam giác ABC.
Tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành.
Tìm trên trục hoành điểm P sao cho tổng khoảng cách từ P tới hai điểm A và B
là nhỏ nhất.
---- Hết ----
ĐÁP ÁN ĐỀ KIỂM TRA HỌC KÌ 1 NĂM HỌC 2019-2020
MÔN TOÁN 10 – ĐỀ CHÍNH THỨC
Câu | Nội dung | Điểm |
Câu 1 1 điểm | Cho hàm số | |
Vì | 0.25 | |
Trục đối xứng | 0.25 | |
Từ (1) và (2) ta có | 0.25 | |
Vậy (P): | 0.25 | |
Câu 2 2 điểm | Giải các phương trình sau: 1) | |
Điều kiện: | 0.25 | |
| 0.25 | |
0.25 | ||
Vậy phương trình có tập nghiệm | 0.25 | |
2) | ||
TH1: Pt có dạng | 0.5 | |
TH2: Pt có dạng | 0.5 | |
Vậy tập nghiệm của phương trình S = | ||
Câu 3 1 điểm | Giải hệ phương trình: | |
Thay (2) vào (1) (1) | 0.25 | |
| 0.5 | |
Vậy hệ phương trình có nghiệm | 0.25 | |
Câu 4 1 điểm | Cho phương trình: | |
Để phương trình có hai nghiệm phân biệt thì | 0.25 | |
Theo định lý Viet, ta có : | 0.25 | |
Ta có:
| 0.25 | |
Vậy m = - 6 thỏa ycbt | 0.25 | |
Câu 5 1 điểm | Tìm giá trị nhỏ nhất của hàm số | |
Vì | 0.25 | |
Áp dụng bất đẳng thức Cauchy ta có: | 0.25 | |
| 0.25 | |
Đẳng thức xảy ra khi và chỉ khi Vậy GTNN của y là | 0.25 | |
Câu 6 2 điểm | 1. Cho hình vuông ABCD có AB = a. Tính theo a các tích vô hướng | |
| 0.25 0,25 | |
Vậy | 0.25 0.25 | |
2. Cho tam giác ABC có | ||
Đặt Ta có nửa chu vi | 0.25 | |
0.25 | ||
0.5 | ||
Vậy | ||
Câu 7 2 điểm | Trong mặt phẳng tọa độ Oxy, cho tam giác ABC biết A(1;4), B(-2; -1) và C(3;1) 1. Tính chu vi tam giác | |
| 0.5 | |
Chu vi tam giác | 0.25 | |
2. Tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành. (0.75 điểm) | ||
Gọi D(x;y) , | 0.25 | |
ABCD là hình bình hành | 0.5 | |
| ||
P nằm trên trục hoành nên Vì A và B nằm về hai phía đối với trục hoành nên
| 0.25 | |
Vậy | 0.25 | |
NỘI DUNG KIỂM TRA HKI MÔN TOÁN 10
Thời gian: 90 phút
Đại số: ( 6 điểm)
Hàm số bậc hai: Tìm a,b,c. ( 1 điểm)
Giải phương trình chứa ẩn dưới mẫu, pt chứa căn, phương trình chứa dấu trị tuyệt đối. ( 2 điểm)
Giải hệ phương trình. ( 1 điểm)
Tìm m thỏa điều kiện về nghiệm của phương trình bậc hai. ( 1 điểm)
Bất đẳng thức. ( 1 điểm)
Hình học: ( 4 điểm)
Tích vô hướng của hai vec tơ. ( 1 điểm)
Hệ thức lượng trong tam giác. ( 1 điểm)
Tọa độ của vecto, tọa độ của điểm; Biểu thức tọa độ tích vô hướng. (2 điểm)

 Trang Trước
Trang Trước





No comments: