bài tập Định Lý Vi-et
1) Cho pt (x+m-2) [x^2 +2(m+2) x+4m-8 ] =0
Tìm m để pt có 2 nghiệm dương và 1 nghiệm âm
2) Cho pt: (2x^2-4x+a+5)(x^2-2x+a) (|x-1|-a-1) =0
Tìm a để pt có đúng 3 nghiệm phân biệt
Tìm m để pt có 2 nghiệm dương và 1 nghiệm âm
2) Cho pt: (2x^2-4x+a+5)(x^2-2x+a) (|x-1|-a-1) =0
Tìm a để pt có đúng 3 nghiệm phân biệt
Giải:
Bài 1: (x+m-2) [x2 +2(m+2) x+4m-8 ] =0
Ta thấy phương trình đã cho luôn có 1 nghiệm x=2-m.
Trong phương trình: x2 +2(m+2) x+4(m-2)=0
Ta có: x1+x2=S=-2(m+2),x1.x2= P=4(m-2)
Đề bài yêu cầu: 2 nghiệm dương, 1 nghiệm âm do đó:
+nếu x=2-m dương=>2-m>0=>2>m
thì còn 1 nghiệm đương và 1 nghiệm âm
=>P<0=>4(m-2)<0=>m<2
Ta thấy m<2 thỏa..
+nếu x=2-m âm=>2-m<0=>2<m
Thì còn 2 nghiệm dương:
=>P>0=>4(m-2)>0=>m>2
Ta thấy mâu thuẫn.
+nếu x=2-m=0=>m=2 thì:
x2 +2(m+2) x+4(m-2)=0<=>x2+4x=0=>x=0 và x=-4
cũng không thỏa yêu cầu bài toán.
Vậy m<2 là giá trị cần tìm.
2) Cho pt: (2x^2-4x+a+5)(x^2-2x+a) (|x-1|-a-1) =0
Tìm a để pt có đúng 3 nghiệm phân biệt
Giải: (2x2-4x+a+5)(x2-2x+a) (|x-1|-a-1) =0
<=>(2x2-4x+2+a+3)(x2-2x+1+a-1) (|x-1|-a-1) =0
<=>[2(x-1)2+a+3][(x-1)2+a-1] (|x-1|-a-1) =0
Ta có các trường hợp sau:
Có 3 nghiệm, thỏa yêu cầu bài toán.
Nếu a=-3 ta có:
Có 3 nghiệm, thỏa yêu cầu bài toán.
Có 3 nghiệm, thỏa yêu cầu bài toán.
Nếu a<-3 thì ta có: a+3<0, a-1<0, -a-1>0,
Hệ có 4 nghiệm, không thỏa yêu cầu bài toán.
Nếu -3<a<-1 thì a+3>0, a-1<0, -a-1>0
Hệ có 2 nghiệm không thỏa yêu cầu bài toán.
Nếu -1<a<1 thì: a+3>0, a-1<0, -a-1<0
ở đây ta xét:
Do đó trong trường hợp này hoặc hệ có 2 nghiệm hoặc có 4 nghiệm nên khoan thỏa yêu cầu bài toán.
Nếu a>1, thì a+3>0, a-1>0, -a-1<0
Hệ có 2 nghiệm, không thỏa yêu cầu bài toán.
Kết luận: a=-3, a=1, a=-1 thỏa yêu cầu đề bài.
Subscribe to:
Post Comments (Atom)





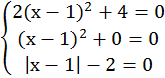








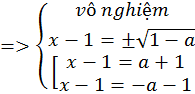


 Trang Trước
Trang Trước





1.
ReplyDeleteThử m=0 xem có đúng không
Dám kl không m thỏa mãn
This comment has been removed by the author.
Deleteuhm, đúng rồi, lúc sáng nhằm m<2.
Delete1.
ReplyDeleteĐsố.m<2
2.
Hướng dẫn
Đặt x-1=t
f(t) đối xứng qua trục tung
có 3 nghiệm =>t=0 phải là nghiệm
•a=-3
•a=+-1
đó cũng là một cách, nhưng lớp 9 giải theo cách này thì dể hiểu hơn.
DeleteThis comment has been removed by the author.
ReplyDelete