Động Hóa Học 2
4. Các qui luật động học đơn giản
Phân loại phản ứng theo bậc n, từ đó dẫn ra các phương trình động học hay biểu thức tốc độ tích phân
4.1. Phản ứng bậc 1
A ® P
· Phương trình động học
| Cách 1 | Cách 2 |
| - lnC = kt + I nếu t = 0 ® C = Co I = -lnCo | Co = a; Ct = a - x - ln(a - x) = kt |
* Qua đại lượng vật lí l = k C
Phản ứng:
C12H22O11 + H2O ¾® C6H12O6 + C6H12O6
Saccaro Gluco Fructo
C ~ a (quay phải) quay phải (a+) quay trái (a-)
Đây là phản ứng bậc n = 1 biểu kiến (chứng minh) và C ~ a.
Ở to = 0 dung dịch có ao ứng với Co (hay a bằng 100% = 1)
t = t at (đã có x% phản ứng Þ C còn lại = 1-x;
C sản phẩm = x + x = 2x)
t = ¥ a¥ (x ® 1, nồng độ sản phẩm = 2x =2)
Ở t = 0 góc quay ao của hỗn hợp phản ứng = góc quay a của saccaro = ao (đo được)
Tại t = t góc quay at = góc quay do saccaro (1 - x) ao + góc quay do sản phẩm 2xasp:
at = (1 - x) ao + 2xasp
Þ at = ao - xao + 2xasp = ao + x(2asp -ao)
Þ x = (at - ao)/ (2asp -ao)
Þ x = (at - ao)/ (a¥ -ao)
Áp vào phương trình phản ứng bậc 1:
Þ lg (at - a¥) = lg (ao - a¥) -  kt
kt
 Xử lí bằng đồ thị ¾® lg (at - a¥)
Xử lí bằng đồ thị ¾® lg (at - a¥)
lg (ao - a¥)
® tga = -k/2,303
4.2. Phản ứng bậc 2
4.2.1. Nồng độ đầu khác nhau
A + B ® P
t = 0 Co = a b 0
t = t C = a-x b - x x
W = + = k (a - x) (b - x) ¾®
= k (a - x) (b - x) ¾®  = kdt
= kdt
Vì tử số = 1 Þ (A + B) = 0 và Ab + Ba = 1.
4.2.2. Nồng độ đầu bằng nhau: Tự dẫn ¾® k = 
 ® t1/2 = 1/(kCo)
® t1/2 = 1/(kCo)
4.3. Phản ứng bậc 3 (xét trường hợp đơn giản nồng độ đầu các chất bằng nhau)
-  = kdt Þ Lấy
= kdt Þ Lấy  hai vế Þ
hai vế Þ  = kt + I
= kt + I
ở t = 0 Þ I =  Þ k =
Þ k = 
 Þ t1/2 = 3/(2kCo2)
Þ t1/2 = 3/(2kCo2)
4.4. Phản ứng bậc n (¹1)
- = kCn ® -
= kCn ® - = kdt ®
= kdt ®  ®
®  = kt + I
= kt + I
4.5. Bậc 0: k = 1/t . (Co- C) Þ t1/2 = Co/2k
4.6. Các phương pháp xác định n, k
4.6.1. Phương pháp thế (thử, mò)
Thường từ thực nghiệm ta có C = f(t)T dưới dạng bảng/ đồ thị.
Lần lượt chọn n = 1, 2, 3,...
Thay vào phương trình tính k, nếu k = const ® n tương ứng.
Ví dụ phản ứng: CH3COOC2H5 + NaOH  CH3COONa + C2H5OH
CH3COONa + C2H5OH
Cho dãy: X = f(t); x = [NaOH] xác định = chuẩn độ.
| t | k1 | k2 |
| 5 | 0,089 | 0,0070 |
| 15 | 0,077 | 0,0067 |
| 25 | 0,060 | 0,0069 |
| 25 | 0,050 | 0,0066 |
| 35 | 0,039 | 0,0067 |
[k] = …..ph-1.mol-1l.
4.6.2. Phương pháp đồ thị
Biến phương trình động học Þ dạng đường thẳng.
n = 1: k =  ln
ln  Þ k =
Þ k =  lnC0 -
lnC0 -  lnC
lnC
Þ lnC = - kt + ln C0 hoặc ln  = kt
= kt
n = 2 : Nếu a ¹ b:
Nếu a = b:  k =
k = 
 ® kt =
® kt =  ®
®  = kt +
= kt + 
Ví dụ: Xác định k và n của phản ứng A ® sản phẩm, biết:
| t, ph | 0 | 0,5 | 1 | 2 | 3 | 4 | 5 |
| CA, mol | 1 | 0,901 | 0,820 | 0,667 | 0,501 | 0,435 | 0,344 |
| lnC | 0 | -0,104 | -0,198 | -0,404 | -0,691 | -0,832 | -1,067 |
Vẽ đồ thị lnC - t: thẳng Þ n = 1
4.6.3. Phương pháp chu kì bán huỷ
Þ lg  = (n - 1) lg
= (n - 1) lg  Þ n - 1 =
Þ n - 1 =  Þ n =
Þ n =  + 1
+ 1
Hoặc biện luận theo cách t1/2 tỉ lệ (hoặc không) với Co.
Ví dụ:
Nồng độ đầu Co giảm 2 lần trong 10'. Nếu tăng Co lên 5 lần, thì sau 24'' còn lại 1/2 lượng chất đầu. n = ?
2. Co tăng 5 lần, t1/2 giảm 25 = 52 lần ® n = 3. Kiểm tra lại:
4.6.4. Qua các đại lượng vật lí (l)
Giải thích, ví dụ l
Xác định k, n qua l:
Cho phản ứng (phương trình tỉ lượng): nA + mB + pC ¾® rZ
Cho l » tuyến tính với C của mỗi cấu tử, khi đó l (có tính cộng tính) bằng
l = lA + lB + lC + lZ + lM (M: môi trường)
Vì l ~ C: lA = kA[A] hoặc li = ki [i]
Gọi a, b, c là nồng độ đầu của A, B, C
x là nồng độ đương lượng đã phản ứng ở t:
lo = lM + kAa + kBb + kCc (1)
l(t) = lM + kA(a - nx) + kB(b - mx) + kC(c - px) + kZ rx (2)
Giả thiết lượng chất A là ít nhất so với C và B, khi đó tại t = ∞ ® [A] = 0
Þ nx = a
Vậy: l¥ = lM + kB + kC
+ kC  + kZ
+ kZ  (3)
(3)
Suy ra: l¥ - lt = (3) - (2) = kZ
l¥ - lo = (3) - (1) = kZ  - kA (a) - kB
- kA (a) - kB  - kC
- kC 
lt - lo = (2) - (1) = kZ (rx) - kA (nx) - kB (mx) - kC (px)
l¥ - lo =  Dk trong đó Dk = kZr - kAn - kBm - kCp
Dk trong đó Dk = kZr - kAn - kBm - kCp
Ví dụ 1: phản ứng phân huỷ axeton:
CH3COCH3 ¾® C2H4 + H2 + CO
| t, ph | 0 | 6,5 | 13,0 | 19,9 |
| P, N.m2 | 41589,6 | 54386,6 | 65050,4 | 74914,6 |
Xác định n, k (V = const).
Giải: CH3COCH3 ¾® C2H4 + H2 + CO
t = 0 Po
t = t Po - x x x x
Þ P = (Po - x) + 3x = Po + 2x Þ x = 
Giả sử phản ứng bậc 1: k =  lg
lg  =
=  =
=  =
= 
Thay số: k1 =  lg
lg 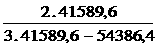 = 0,0256 ph-1
= 0,0256 ph-1
Ví dụ 2: Thuỷ phân: C12H22O11 + H2O ¾® C6H12O6 + C6H12O6
t = 0 a0 ~ 1 phần (0) (0)
 t = t ~ (1 - x) phần x x ® at t = ¥ a¥
t = t ~ (1 - x) phần x x ® at t = ¥ a¥
Ở t = 0 góc quay ao của hỗn hợp phản ứng = góc quay a của saccaro = ao (đo được)
Tại t = t góc quay at = góc quay do saccaro (1 - x) ao + góc quay do sản phẩm 2xasp: at = (1 - x) ao + 2xasp
Þ at = ao - xao + 2xasp = ao + x(2asp -ao)
Þ x = (at - ao)/ (2asp -ao) Þ x = (at - ao)/ (a¥ -ao)
Phản ứng là bậc 1 (biểu kiến):
Ví dụ 3: (CH3)3COOC(CH3)3  CH3COCH3 + C2H6
CH3COCH3 + C2H6
Peroxitbutyl bậc 3 axeton etan
Đo P theo t (………). Xác định k, n ?
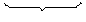
Giả sử: k =  ln
ln  =
=  lg
lg  (áp dụng hệ thức trên)
(áp dụng hệ thức trên)
Đã có: Po
Pt
P¥ (hoặc thực nghiệm, hoặc tình từ Po: 3Po = P¥
 Þ kt = 2,303 lg (P¥ - Po) - 2,303 lg (P¥ - Pt)
Þ kt = 2,303 lg (P¥ - Po) - 2,303 lg (P¥ - Pt)
Þ lg (P¥ - Pt) = - t + lg (P¥ - Po)
t + lg (P¥ - Po)
k = 2,09.10-2 ph-1
Có thể xác định từ đồ thị như hình bên:
4.6.5. Phương pháp cô lập và tốc độ đầu.
LgW0,1 = lgk + nlgC0,1
LgW0,2 = lgk + nlgC0,2
 4.6.6. Phương pháp phân tích đường cong. (tr. 49, sgk)
4.6.6. Phương pháp phân tích đường cong. (tr. 49, sgk)
* Nếu có một đường cong
C = a C0 ®  = C0
= C0  ®
®  =
= 
 ® -
® - = k
= k  . an
. an
lg  = lg
= lg = (1 - n) lg a1 = (1 - n) lg
= (1 - n) lg a1 = (1 - n) lg  ® (1 - n) =
® (1 - n) = 
Ví dụ 1.
| t, s | 0 | 20 | 40 | 60 | 80 |
| [NO2].1011 mol/l | 17,6 | 10,6 | 7,1 | 5,4 | 4,6 |
a2 = (0,595)2 = 0,354
Þ C2 = 0,354 . 17,8 = 6,35 ® t2 = 50"
* Nếu có 2 đường cong:
W = -dC/dt = kCn = k(Co a)n
Þ có 2 thì n ghiệm ứng với: C0,1 và C0,2
Đặt (1) = (2): Þ k (C0,1)n-1 t1 = k (C0,2)n-1 t2 Þ n = 1 + 
Ví dụ 2. Phân huỷ đioxan:
P0,1 = 800 mmHg ® t1/2, 1 = 13,9'
P0,2 = 400 mmHg ® t1/2, 2 = 19'











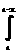
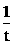



























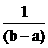























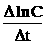


















































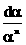









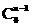

































 Trang Trước
Trang Trước





No comments: