Hướng Dẫn Giải Toán Lớp 8 HKII Trường Trần Quốc Toản
Câu 1 (4 điểm): Giải các phương trình sau.
a) 12-6x=4(2x+3)
Câu 2 (1,5 điểm): Giải các bất phương trình và biểu diễn tập nghiệm trên trục số.
Câu 3 (1 điểm) Giải bài toán bằng cách lập phương trình.
Hiệu của hai số là 16 và số lớn gấp 5 lần số bé. Tìm hai số đó?
Câu 4 (3,5 điểm): Cho tam giác ABC vuông tại A có đường cao AH và đường phân giác trong BD.
a) Chứng minh:  Suy ra: AH.BC=AB.AC.
Suy ra: AH.BC=AB.AC.
c) Qua C vẽ đường thẳng a song song với BD, từ B kẻ BE  a (E
a (E  a), đường thẳng BE cắt đường thẳng AC tại F. Chứng minh: DA.FC=DC.FA
a), đường thẳng BE cắt đường thẳng AC tại F. Chứng minh: DA.FC=DC.FA
Giải
Câu 1:
a) 12-6x = 4(2x+3)
Câu 2:
Câu 3:
Gọi x là số bé.
Suy ra số lớn: 5x
Theo đề bài ta có:
5x-x=16
4x=16
X=4
Số lớn: 5x=5.4=20
Câu 4:
a. Xét hai tam giác BAH và BCA ta có:
b. Vì BD là phân giác của tam giác ABC. Nên Áp dụng tính chất dường phân giác ta có:
Kết hợp với (*) ta được:
c.
Giải:
Ta có:
Vậy BF là tia phân giác ngoài của góc B.
Áp dụng tính chất phan giác ta có:
Kết hợp với (*) ta được:
=>DA.FC=FA.DC
d. dể thấy hai tham giác FAB và FEC đồng dạng, vì hai tam giác vuông có chung gốc F.
Xét hai tam giác FAE và FBC ta có:
Gốc F chung


















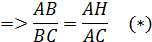















 Trang Trước
Trang Trước


No comments: