TRƯỜNG ĐẠI HỌC SÀI GÒN          ĐỀ THI KẾT THÚC MÔN HỌC                         Môn thi: Qui hoạch tuyến tính                                    Lớp: CKE  

                                                             Thời gian làm bài: 90 phút

Sinh viên không được tham khảo tài liệu để làm bài

Bài 1. Một xí nghiệp sản xuất ba mặt hàng . Việc sản xuất được thực hiện theo dây chuyền trên ba máy . Tiền khấu hao mỗi giờ (tính bằng USD) trên mỗi loại máy lần lượt là 2, 1, 3. Thời gian hoạt động tối đa của các máy trong tuần (tính theo giờ) lần lượt là 120, 100 và 80. Thời gian cần thiết đối với các máy (tính theo giờ) để sản xuất một đơn vị mặt hàng được cho bởi bảng sau:

Nguyên liệu được cung cấp tối đa để sản xuất là 250 đơn vị (đv). Lượng nguyên liệu cần thiết để sản xuất một đơn vị mặt hàng các loại lần lượt là 5đv, 3đv, 4đv. Chi phí về chuyên chở, về tiền công và giá bán mỗi đơn vị mặt hàng các loại (tính bằng USD) được cho trong bảng sau:

Yêu cầu:

1.     Tính lợi nhuận thu được trên mỗi đơn vị mặt hàng.

2.     Lập bài toán qui hoạch tuyến tính để xí nghiệp sản xuất đạt lợi nhuận cao nhất trong tuần.

3.     Lập bài toán đối ngẫu của bài toán trên.

4.     Tìm phương án tối ưu của cả hai bài toán.

Bài 2. Cần vận chuyển một loại hàng từ bốn kho hàng đến nơi tiêu thụ (cửa hàng). Số lượng đơn vị hàng ở các kho tương ứng là , số lượng đơn vị hàng cần có ở các cửa hàng là  và cước phí vận chuyển một đơn vị hàng từ kho thứ i đến cửa hàng thứ j cho bởi ma trận sau:

Hãy lập kế hoạch vận chuyển hàng sao cho đảm bảo cung cầu và cước phí vận chuyển nhỏ nhất.

Bài giải.

1.     Tính lợi nhuận thu được trên mỗi đơn vị mặt hàng

Lợi nhuận = Giá bán – Tổng các chi phí

LN1=25 – (2.4+1.1+3.2+3+3)=5

LN2=21 – (2.3+1.3+3.1+1+2)=6

LN3=20 – (2.1+1.2+3.1+2+3)=8

2.     Lập bài toán quy hoạch tuyến tính

Gọi  lần lượt là số lượng các mặt hàng cần sản xuất ()

Lợi nhuận thu được cao nhất khi  đạt max

Thời gian sử dụng máy

          :  không vượt quá 120

          :  không vượt quá 100

          :  không vượt quá 80

Nguyên liệu sử dụng

          không vượt quá 250

Mô hình: Tìm  thoả

                                                                       (P)

3.     Lập bài toán đối ngẫu

(D)

4.     Tìm phương án tối ưu của cả hai bài toán.

Chọn bài toán (P) để giải

Đưa bài toán về dạng chính tắc

          Lập bảng đơn hình

Phương án tối ưu của bài toán (P) là  và .

Suy ra phương án tối ưu của bài toán (D):   và .

Bài 2.

·        Kiểm tra điều kiện cân bằng thu phát, ta có .

·        Xây dựng phương án ban đầu:

·        Kiểm tra tính tối ưu, ta thấy .

·        Xây dựng phương án mới:

·        Kiểm tra tính tối ưu, ta thấy 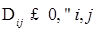. Ta có phương án tối ưu của bài toán:

, và đơn vị tiền tệ.

Câu 1. Một xí nghiệp có thể sàn xuất bốn loại mặt hàng xuất khẩu H₁, H₂, H₃ và H₄. Để sản xuất 4 loại mặt hàng này, xí nghiệp sử dụng 2 loại nguyên liệu N₁ và N₂. Số nguyên liệu tối đa mà xí nghiệp huy động được tương ứng là 600kg và 800kg. Mức tiêu hao mỗi loại nguyên vật liệu để sản xuất một mặt hàng và lợi nhuận thu được cho trong bảng sau:

Yêu cầu

1.     Hãy lập mô hình để xí nghiệp sản xuất đạt lợi nhuận cao nhất;

2.     Xây dựng bài toán đối ngẫu ứng với mô hình toán ở câu 1.;

3.     Áp dụng thuật toán đơn hình cải tiến và kết quả đối ngẫu để tìm các phương án tối ưu cho cả 2 mô hình.

Câu 2. Cần vận chuyển một loại hàng từ kho hàng  đến nơi tiêu thụ (cửa hàng). Số lượng đơn vị hàng từ các kho tương ứng là ; số lượng hàng từ các của hàng là  và cước phí vận chuyển một đơn vị hàng từ kho thứ i đến cửa hàng thứ j cho bởi ma trận sau

1.     Hãy lập kế hoạch vận chuyển hàng