XÁC SUấT THốNG KÊ B
TRƯỜNG ĐẠI HỌC SÀI GÒN ĐỀ THI KẾT THÚC MÔN HỌC
HỆ CAO ĐẲNG CHÍNH QUY
Hoc kỳ I – Năm học 2010-2011
Môn thi: XÁC SUấT THốNG KÊ B
Thời gian làm bài: 90 phút
Sinh viên không được tham khảo tài liệu để làm bài
Câu 1. Một trạm tín hiệu chỉ phát hai loại tín hiệu A và B với xác suất tương ứng là 0,8 và 0,2. Do có nhiễu trên đường truyền nên 1\6 tín hiệu A bị méo và thu được như tín hiệu B, còn 1\8 tín hiệu B bị méo thành tín hiệu A.
a) Tìm xác suất thu được tín hiệu A.
b) Giả sử thu được tín hiệu A, tìm xác suất để thu được đúng tín hiệu lúc phát.
Câu 2. Một lô hàng gồm 5 sản phẩm loại A và 15 sản phẩm loại B. Lấy ngẫu nhiên cùng một lúc 4 sản phẩm để kiểm tra.
a) Tính xác suất để trong 4 sản phẩm lấy ra có đúng 3 sản phẩm loại A.
b) Gọi X là số sản phẩm loại B có trong 4 sản phẩm lấy ra, hãy lập phân phối xác suất của X.
c) Tính kỳ vọng và phương sai của đại lượng ngẫu nhiên X.
Câu 3. Điều tra điểm môn Triết học của một trường Đại học ta có số liệu thống kê sau:
Điểm (X) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Số sinh viên(mi) | 12 | 18 | 39 | 25 | 70 | 65 | 100 | 72 | 7 | 10 |
a) Hãy ước lượng điểm trung bình môn Triết học của sinh viên trường Đại học trên ở độ tin cậy 98%.
b) Biết sinh viên trường đó có điểm trung bình môn Toán cao cấp là 5.55. Hãy so sánh điểm trung bình môn Triết học với điểm trung bình môn Toán cao cấp với mức ý nghĩa 
.
c) Có một kết luận cho rằng tỉ lệ sinh viên thi qua môn Triết học của trường Đại học này là 60%. Theo bạn, điều đó đúng không (kết luận ở 
)?
TRƯỜNG ĐẠI HỌC SÀI GÒN ĐỀ THI KẾT THÚC MÔN HỌC
HỆ CAO ĐẲNG CHÍNH QUY
Hoc kỳ I – Năm học 2010-2011
Môn thi: Xác suất thống kê B
Thời gian làm bài: 90 phút
Sinh viên không được tham khảo tài liệu để làm bài
Bài 1. Trong một kiện hàng có 42% sản phẩm do nhà máy A sản xuất, 24% sản phẩm do nhà máy B sản xuất, 26% sản phẩm do nhà máy C sản xuất và 8% sản phẩm do nhà máy D sản xuất. Trong đó có một số sản phẩm bị lỗi gồm: 10% của nhà máy A sản xuất, 5% của nhà máy B sản xuất, 6% của nhà máy C sản xuất và 1% của nhà máy D sản xuất. Chọn ngẫu nhiên một sản phẩm trong kiện hàng đó, hãy:
a) Tính xác suất để sản phẩm chọn ra là sản phẩm bị lỗi;
b) Biết sản phẩm chọn ra là sản phẩm bị lỗi. Tính xác suất để sản phẩm đó là của nhà máy C sản xuất.
Bài 2. Một thùng gồm 10 sản phẩm, trong đó có 3 sản phẩm loại I và 7 sản phẩm loại II. Lấy ngẫu nhiên 4 sản phẩm bày làm mẫu (không bán) còn lại đem ra cửa hàng bày bán.
a) Hãy tính xác suất để trong các sản phẩm bày làm mẫu có đúng 2 sản phẩm loại I.
b) Hãy lập bảng phân phối xác suất cho các sản phẩm loại II có trong các sản phẩm bày bán.
Câu 3. Một xạ thủ có xác suất bắn trúng đích mỗi phát là 0,7. Xạ thủ này bắn 100 phát vào bia. Tính xác suất để:
a) Có 60 phát trúng bia;
b) Có từ 60 đến 80 phát trung bia;
c) Có không dưới 80 phát trung bia.
Câu 4. X(kg) là 1 chỉ tiêu của một loại sản phẩm thuộc xí nghiệp A. điều tra một số sản phẩm của xí nghiệp này có kết quả sau:
xi | 50 – 55 | 55 – 60 | 60 – 65 | 65 – 70 | 70 – 75 | 75 – 80 |
ni | 5 | 10 | 25 | 30 | 18 | 12 |
a) Ước lượng trung bình chỉ tiêu X với độ tin cậy 92%.
b) Muốn ước lượng trung bình chỉ tiêu X với độ tin cậy 95% và với độ chính xác không quá 1kg, có cần bổ sung mẫu không? Nếu có, bằng bao nhiêu?
c) Có một tài liệu nói trung bình chỉ tiêu X bằng 70(kg). Cho nhận xét ở mức ý nghĩa 5%.
ĐÁP ÁN:
Đề 01.
Câu 1.
a) Gọi 
: trạm phát phát tín hiệu A; 
: trạm phát phát tín hiệu B.
H: Biến cố thu được tín hiệu A.
Ta có:
b) Ta có:
.
Câu 2.
a) Gọi A: biến cố 4 sp lấy ra trong đó có 3 sp loại A.
Ta có 
.
b) Ta có: 
.
X | 0 | 1 | 2 | 3 | 4 |
P(X) |
|
|
|
|
Câu 3. Ta có :
.
a) Gọi 
: điểm trung bình môn Triết của trường Đại học.
Ta tìm 
. Với 
. Ta có 
.
Vậy 
.
b) Giả thiết H: 
.
Ta có:
.
.
Tạm bác bỏ giả thiết H. mà 
.
Vậy điểm tung bình môn Triết > điểm trung bình môn Toán cao cấp.
c) Gọi 
tỉ lệ thi đậu môn Triết, ta có 
. p: tỉ lệ thi đậu môn triết của trường.
Đặt giả thiết H: 
.
Với 
.
Ta có 
.
Tạm bác bỏ giả thiết H.
Đáp án XSTK A:
Câu 1.
Gọi 
lần lượt là các biến cố sp do nhà máy A, B, C, D sản xuất.
H: Biến cố sp chọn ra bị lỗi.
a) Ta có 
là nhóm 4 biến cố đầy đủ. Áp dụng công thức xác suất đầy đủ, ta có:
.
b) Ta có: 
.
Câu 2. Gọi A: biến cố trong 4 sp chọn làm mẫu có 2 sp loại I.
a) Ta có: 
.
b) Gọi X là số sp loại II có trong các sản phẩm bày bán. X nhận các giá trị 3,4,5,6.
Ta có: 
với 
.
Bảng phân phối:
X | 3 | 4 | 5 | 6 |
P(X) | 35/210 | 105/210 | 63/210 | 7/210 |
Câu 3.
Gọi X là số phát đạn bắn trung trong 100 phát, ta có: 
với 
nên 
; 
a) 
;
b) 
;
c) 
Bài 4. Gọi X là số giờ tự học trung bình của sinh viên trong mẫu.
là số giờ tự học trung bình của sinh viên toàn trường.
Ta có 
.
Do đó 
.
1. Ước lượng số giờ học trung bình của sinh viên trong tuần là 6,32 giờ.
2. Với 
, ta có 
.
Do đó 
.
Vậy 
giờ.
3. Đặt giả thiết 
;
Ta có 
.
Tính 
Do đó ta bác bỏ giả thiết. Vậy số giờ tự học của sinh viên < 8 giờ.
Tags: Đại Học Sài Gòn, Hóa Học hay, Hóa Học Khó, SGU
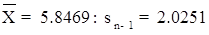
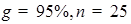
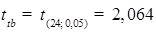
Trang Trước
No comments: