Câu 5 - Toán Cao Cấp - Trần Thanh Bình - Đại Học Sài Gòn
Câu 5: Định a, b để hàm số liên tục trên R:
· Trên  , hàm số y trùng với
, hàm số y trùng với  . Vì y là hàm sơ cấp xác định với mọi
. Vì y là hàm sơ cấp xác định với mọi  nên hàm số y lien tục trên
nên hàm số y lien tục trên 
· Trên  , hàm số y trùng với
, hàm số y trùng với  . Vì y là hàm sơ cấp xác định với mọi
. Vì y là hàm sơ cấp xác định với mọi  nên hàm số y lien tục trên
nên hàm số y lien tục trên 
Suy ra
Y liên tục trên R  y lien tục tại x=2
y lien tục tại x=2
Như vậy:
Y liên tục trên R
Như vậy, không tồn tại a để hàm số đã cho liên tục trên R
· Trên  hàm số y trùng với
hàm số y trùng với  . Vì y là hàm sơ cấp xác định với mọi x khác 1 và 2 nên hàm số y liên tục trên
. Vì y là hàm sơ cấp xác định với mọi x khác 1 và 2 nên hàm số y liên tục trên .
.
· Trên [ 1,2 ] hàm số y trùng với  . Vì y là hàm sơ cấp xác định với mọi
. Vì y là hàm sơ cấp xác định với mọi  nên hàm số y liên tục trên [ 1,2 ].
nên hàm số y liên tục trên [ 1,2 ].
· Trên  hàm số y trùng với
hàm số y trùng với  . Vì y là hàm sơ cấp xác định với x<2 nên hàm số y liên tục trên
. Vì y là hàm sơ cấp xác định với x<2 nên hàm số y liên tục trên  .
.
Suy ra
Từ (1), (2), (3) ta suy ra:


















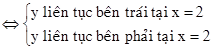





 Trang Trước
Trang Trước



No comments: