Hình Học 9 - Tuấn Anh
Hình Học 9 - Ngốc Nghếch Lắm
Cho đường tròn (O:R) và điểm A nằm ngoài đường tròn sao cho OA= R nhân căn bậc 2. Từ A vẽ các tiếp tuyến AB, Ac với đường tròn(B,C là các tiếp điểm). Lấy D thuộc AB: E thuộc AC sao cho chu vi của tam giác bằng 2R.
a) Cm tứ giác ABOC là hình vuông.
b) Cm DE là tiếp tuyến của đường tròn (O:R)
c) Tìm giá trị lớn nhất của diện tích tam giác ADE.
p/s: m.n làm nha, có j giúp mình với...
Giải:
a.chứng minh AB,OC là hình vuông:
áp dụng hệ thức lượng giác vào tam giác ABO ta được:
=>  =45 (tính chất 2 tiếp tuyến cắt nhau
=45 (tính chất 2 tiếp tuyến cắt nhau
=>tứ giác ABOC là hình chử nhật (có 3 góc vuông)
Lại có: OA BC (tính chất 2 tiếp tuyến cắt nhau) – cái này nếu trường em nào không chịu thì chứng minh OA là đường trung trực của BC nhé.
BC (tính chất 2 tiếp tuyến cắt nhau) – cái này nếu trường em nào không chịu thì chứng minh OA là đường trung trực của BC nhé.
Vậy: ABOC là hình vuông (hình chử nhật có 2 đường chéo vuông góc)
b. chứng minh DE là tiếp tuyến của (O)
ü Nếu DE là tiếp tuyến: gọi tiếp điểm là F
Ta có:
ü BD=DF (tính chất 2 tiếp tuyến cắt nhau)
ü EF=CE (tính chất 2 tiếp tuyến cắt nhau)
Ta xét chu vi:
PADE=AD+AE+DE
=AD+AE+DB+EC
=AD+DB+AE+EC
=AB+AC=R+R=2R (do tứ giác ABOC là hình vuông nên mỗi cạnh đều có chiều dài là R)
Ta thấy thỏa yêu cầu bài toán.
v Nếu DE không phải là tiếp tuyến, sẽ có 2 trường hợp:
Ø Trường hợp 1: DE vào (O) không có điểm chung)
Vẽ tiếp tuyến DK:
Chứng minh tương tự như trên ta có:
PADK=2R
Do đó: PADE<PADK => PADE<2R không thỏa yêu cầu bài toán.
Ø Trường hợp 2: DE và O cắt nhau tạo 2 điểm.
Vẽ tiếp tuyến DK
Tương tự ta có:
PADK=2R
Do đó: PADE>PADK => PADE>2R không thỏa yêu cầu bài toán.
Kết luận: DE phải là tiếp tuyến của đường tròn thì chu vi ADE mới bằng 2R.
c. tim2 giá trị lớn nhất của SADE:
có 2 cách làm:
Cách 1: sử dụng tính chất đại số.
Ta có:
Ta lấy 2ab lớn nhất khi a=b
Áp dụng vào ta được:
Vậy SADE lớn nhất khi AD=AE
=>ADE là tam giác vuông cân, từ đây dể tính được
Cách 2:
Theo câu b ta có:
PADE=AD+AE+DE=2R
=>AD+AE+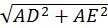 =2R (áp dụng pitago vào tam giác vuông ADE)
=2R (áp dụng pitago vào tam giác vuông ADE)
=>AD2+AE2=4R2-4R(AD+AE)+(AD+AE)2.
=> AD2+AE2+2AD.AE-2AD.AE=4R2-4R(AD+AE)+(AD+AE)2.
=>(AD+AE)2-2AD.AE=4R2-4R(AD+AE)+(AD+AE)2.
=>-2AD.AE=4R2-4R(AD+AE).
=>2AD.AE=-4R2+4R(AD+AE)
AD.AE=-2R2+2R(AD+AE)
ở đây R là số không đổi nên AD.AE lớn nhất khi AD+AE lớn nhất
=>DE nhỏ nhất.
Mà DE nhỏ nhất khi ADE là tam giác cân tại A.
=>ADE vuông cân.
Tới đây giải như trên ta được:
Hết
Lưu ý: ở đây Thầy trình bài 2 cách giải đề mấy em có nhiều lựa chọn trong việc học hơn, và hơn nữa tùy trường mà kiến thức sẽ khác nhau, nen em hãy tự chọn cách thích hợp nhé. Còn nếu em nào có cách giải hay hơn thì cứ comment phía dưới để mọi người tham khảo.
Chúc mấy đứa có chủ nhật thật vui vẽ.




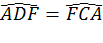





















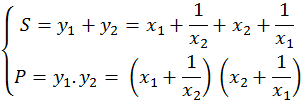












 Trang Trước
Trang Trước


