các bất đẳng thức quan trọng
1. Bunyakovsky
Bất đẳng thức Bunyakovsky dạng thông thường
· (a² + b²)(c² + d²) ≥ (ac + bd)²
· Bất đẳng thức này dễ dàng chứng minh bằng cách khai triển, rút gọn và biến đổi thành: (ad - bc)² ≥ 0
Bất đẳng thức Bunyakovsky cho 2 bộ số
· Dấu "=" xảy ra khi và chỉ khi với quy ước nếu một số
nào đó (i = 1, 2, 3,..., n) bằng 0 thì
tương ứng bằng 0.
hai
2. Bất đẳng thức Bernoulli
Trong toán học, bất đẳng thức Bernoulli là một bất đẳng thức cho phép tính gần đúng các lũy thừa của 1 + x.
Bất đẳng thức này được phát biểu như sau:
với mọi số nguyên r ≥ 0 và với mọi số thực x > −1. Nếu số mũ r là chẵn, thì bất đẳng thức này đúng với mọi số thực x. Bất đẳng thức này trở thành bất đẳng thức nghiêm ngặt như sau:
với mọi số nguyên r ≥ 2 và với mọi số thực x ≥ −1 với x ≠ 0.
Các bất đẳng thức liên quan
Bất đẳng thức dưới đây ước lượng lũy thừa bậc r của 1 + x theo chiều khác. Với số thực x bất kỳ, r > 0, chúng ta có
với e = 2.718.... Bất đẳng thức này có thể chứng minh bằng cách dùng bất đẳng thức (1 + 1/k)k < e.
3. Bất đẳng thức Cauchy
Trong toán học, bất đẳng thức Cauchy, bất đẳng so sánh giữa trung bình cộng và trung bình nhân của n số thực không âm được phát biểu như sau:
Trung bình cộng của n số thực không âm luôn lớn hơn hoặc bằng trung bình nhân của chúng, và trung bình cộng chỉ bằng trung bình nhân khi và chỉ khi n số đó bằng nhau.
· Với 2 số:
Đẳng thức xảy ra khi và chỉ khi
· Với n số:
Đẳng thức xảy ra khi và chỉ khi
Trung bình có hệ số
Cho n số x1, x2, ..., xn ≥ 0
và các hệ số α1, α2, ..., αn > 0.
Bất đẳng thức trung bình cộng và trung bình nhân cũng đúng nếu hai giá trị trung bình có hệ số, như sau:
Dấu " = " xảy ra khi và chỉ khi
Với các loại trung bình khác
4. Bất đẳng thức Cauchy-Schwarz
Bất đẳng thức này phát biểu rằng nếu x và y là các phần tử của không gian tích trong thực hay phức thì
Dấu đẳng thức xảy khi và chỉ khi x và y phụ thuộc tuyến tính (hay nói theo ý nghĩa hình học là chúng song song với nhau). Một trường hợp đặc biệt nữa của x và y là khi chúngtrực giao (hay nói theo ý nghĩa hình học là vuông góc ) nhau thì tích trong của chúng bằng zero.
Một dạng khác của bất đẳng thức Cauchy-Schwarz được phát biểu dưới đây bằng cách dùng ký hiệu chuẩn, với chuẩn ở đây được hiểu là chuẩn trên không gian tích trong
5. Bất đẳng thức cộng Chebyshev
Trong toán học, Bất đẳng thức cộng Chebyshev, được đặt theo tên nhà toán học Pafnuty Chebyshev, được phát biểu rằng: Nếu cho
và
thì
Tương tự, nếu
và
thì
6.Bất đẳng thức Fano
Bách khoa toàn thư mở Wikipedia
Trong lý thuyết thông tin, bất đẳng thức Fano liên hệ lượng thông tin bị mất trên một kênh nhiễu với xác suất phân loại sai. Nó được tìm ra bởi Robert Fano đầu thập niên 1950 khi đang dạy một semina tiến sĩ về lý thuyết thông tin tại MIT, và sau đó được đưa vào cuốn sách năm 1961 của ông.
Nó được dùng để tìm ra một chặn dưới cho xác suất lỗi của bất kì bộ giải mã nào.
Bất đẳng thức Fano
Đặt các biến ngẫu nhiên X và Y đại diện cho thông điệp vào và ra (trong số r+1 thông điệp có thể) với xác suất hợp . Bất đẳng thức Fano là
trong đó
là xác suất lỗi, và
là entropy nhị phân tương ứng.
7.Bất đẳng thức Golden–Thompson
Trong toán học, bất đẳng thức Golden–Thompson, chứng minh độc lập bởi Golden (1965) và Thompson (1965), khẳng định rằng với mọi ma trận Hermit A và B,
trong đó tr là vết của ma trận, và eA là lũy thừa ma trận.
8.Bất đẳng thức Harnack
Bách khoa toàn thư mở Wikipedia
Bất đẳng thức Harnack là một bất đẳng thức bắt nguồn từ giải tích.
Cho là một quả cầu mở và f là một hàm điều hòa trên D sao cho f(z) không âm với mọi
. Khi đó bất đẳng thức sau đúng với mọi
:
Đối với miền tổng quát bất đẳng thức được phát biểu như sau: Nếu
là hàm khả vi hai lần, điều hòa và không âm,
là một miền bị chặn với
, thì sẽ có một hằng số
không phụ thuộc vào
sao cho

9.Bất đẳng thức Hölder
Trong giải tích toán học, bất đẳng thức Hölder, đặt theo tên của nhà toán họcĐức Otto Hölder, là một bất đẳng thức cơ bản liên quan đến các không gian Lp: giả sử S là mộtkhông gian đo, với 1 ≤ p, q ≤ ∞ thỏa 1/p + 1/q = 1, đồng thời f thuộc Lp(S) và g thuộc Lq(S). Khi đó fg thuộc L1(S) và
Các số p và q nói trên được gọi là liên hợp Holder của lẫn nhau.
Bất đẳng thức Holder được dùng để chứng minh bất đẳng thức tam giác tổng quát trong không gian Lp, bất đẳng thức Minkowski và cũng dùng để chứng minh Lp là đối ngẫu với Lq.
Các trường hợp đặc biệt đáng chú ý
· Với p = q = 2 bất đẳng thức Holder trở thành bất đẳng thức Cauchy-Schwarz.
· Trong trường hợp không gian Euclide, khi tập S là {1,...,n} với một độ đo kiểu đếm, chúng ta có kết quả là với mọi x, y trong Rn (Cn)
· Nếu S=N với một độ đo kiểu đếm, khi đó chúng ta có được bất đẳng thức Holder cho các dãy từ không gian lp
· Trong trường hợp không gian của các hàm giá trị phức khả tích, chúng ta có
· Trong trường hợp không gian xác suất ,
là các ký hiệu để chỉ không gian của các biến ngẫu nhiên với momentp hữu hạn,
, trong đó
là ký hiệu chỉ giá trị kỳ vọng. Bất đẳng thức Holder trở thành
Trường hợp tổng quát
Có thể chứng minh trường hợp tổng quát sau bằng phương pháp quy nạp
10.Bất đẳng thức Jensen
Với mọi hàm lồi trên
và mọi
ta có
.
Với mọi hàm lõm trên
và mọi
ta có
.
Lưu ý: là hàm lồi khi ta có
> 0 trên
và là hàm lõm khi ta có
< 0 trên
Bất đẳng thức Jensen là trường hợp đặc biệt của bất đẳng thức Karamata.
11.Bất đẳng thức Newton
Bất đẳng thức Newton được đặt theo tên của nhà toán học và vật lý học thiên tài người Anh Isaac Newton. Nếu cho a1,.........,an là các số thực và cho σk là hàm đối xứng cơ bản thứ k trong các số a1,.........,an thì các giá trị trung bình đối xứng cơ bản, được tính bởi
Sk = σk/(nk)
thỏa mãn bất đẳng thức
Sk-1Sk+1 ≤ S2k
(Trường hợp xảy ra đẳng thức: khi và chỉ khi các số thực a1,.........,an đều bằng nhau)
12.Bất đẳng thức Schur
Trong toán học, bất đẳng thức Schur, đặt tên theo Issai Schur, phát biểu rằng với là các số thực không âm và một số dương
, ta có bất đẳng thức sau:
dấu đẳng thức xảy ra khi và chỉ khi a = b = c hoặc hai trong số chúng bằng nhau và số còn lại bằng không. Khi r là một số nguyên dương chẵn, thì bất đẳng thức trên đúng với mọi số thực a, b, và c.
13.Bất đẳng thức tam giác
Trong toán học, bất đẳng thức tam giác là một định lý phát biểu rằng trong một tam giác chiều dài của một cạnh phải nhỏ hơn tổng, nhưng lớn hơn hiệu, của hai cạnh còn lại.
Bất đẳng thức là một định lý trong các không gian như hệ thống các số thực, tất cả các không gian Euclide, các không gian Lp (p≥1) và mọi không gian tích trong. Bất đẳng thức cũng xuất hiện như là một tiên đề trong định nghĩa của nhiều cấu trúc trong giải tích toán học và giải tích hàm, chẳng hạn trong các không gian vectơ định chuẩn và các không gian metric.
14.Giới hạn Singleton
Trong lý thuyết mã hóa, giới hạn Singleton, đặt theo tên của Richard Collom Singleton, là một giới hạn trên cho kích thước của mã khối với độ dài
, kích thước
, và khoảng cách
(mỗi mã tự có độ dài
, dùng để biểu diễn một thông điệp có độ dài
, và hai mã tự khác nhau có ít nhất
kí hiệu khác nhau).
Phát biểu của giới hạn Singleton
Khoảng cách của một tập bao gồm các mã tự có độ dài
được định nghĩa như sau:
trong đó là khoảng cách Hamming giữa
và
. Biểu thức
biểu diễn số lượng mã tự tối đa của một mã khối có độ dài
, khoảng cách
, và sử dụng kí hiệu trong một bảng chữ cái kích thước
.
Giới hạn Singleton khẳng định rằng
15.Bất đẳng thức Minkowski
Trong giải tích toán học, bất đẳng thức Minkowski dẫn đến kết luận rằng các không gian Lp là các không gian vector định chuẩn. Giả sử S là một không gian đo, giả sử 1 ≤ p ≤ ∞, đồng thời f và g là các phần tử của Lp(S). Khi đó f + g cũng thuộc Lp(S), và chúng ta có
dấu đẳng thức xảy ra chỉ khi f và g phụ thuộc tuyến tính.
Bất đẳng thức Minkowski chính là bất đẳng thức tam giác trong Lp(S). Có thể chứng minh nó bằng cách dùng bất đẳng thức Holder.
Cũng như bất đẳng thức Holder, có thể đưa bất đẳng thức Minkowski về các trường hợp đặc biệt cho các dãy và các vector bẳng cách dùng khái niệm độ đo kiểu đếm được:
với mọi số thực (hay số phức) x1, ..., xn, y1, ..., yn và n là số chiều của S.
16.Bất đẳng thức Nesbitt
Trong toán học, bất đẳng thức Nesbitt là một trường hợp đặc biệt của bất đẳng thức Shapiro khi số phần tử là 3. Nó được phát biểu như sau:
Cho a,b,c là ba số thực dương. Khi đó ta có:
17.Bất đẳng thức Azuma
Trong lý thuyết xác suất, bất đẳng thức Azuma–Hoeffding (đặt tên theo Kazuoki Azuma và Wassily Hoeffding) là một bất đẳng thức về sự tập trung của giá trị một martingale có gia số bị chặn.
Giả sử { Xk : k = 0, 1, 2, 3, ... } là một martingale (hoặc super-martingale) và
gần như chắc chắn. Khi đó, với mọi số nguyên dương N và mọi số thực dương t,
Nếu X là một martingale, thì bằng cách áp dụng bất đẳng thức Azuma cho cả martingale -X và X ta có bất đẳng thức sau:
Bất đẳng thức Azuma áp dụng cho martingale Doob chính là phương pháp gia số bị chặn thường được dùng để phân tích thuật toán ngẫu nhiên.
Bất đẳng thức Hoeffding
Bách khoa toàn thư mở Wikipedia
Trong lý thuyết xác suất, bất đẳng thức Hoeffding cho một chặn trên của xác suất một tổng các biến ngẫu nhiên sai lệch với giá trị kỳ vọng. Bất đẳng thức Hoeffding được chứng minh bởi Wassily Hoeffding.
Giả sử
là các biến ngẫu nhiên độc lập. Giả sử gần như chắc chắn bị chặn; nghĩa là, với mọi
ta có
Giá trị trung bình thực nghiệm của các biến đó là
Ta có các bất đẳng thức sau (Hoeffding 1963, định lý 2 [1]):
cho mọi giá trị t dương. Ở đây là giá trị kỳ vọng của
.
Các bất đẳng thức này là trường hợp đặc biệt của bất đẳng thức Azuma–Hoeffding và của một bất đẳng thức tổng quát hơn nữa là bất đẳng thức Bernstein trong lý thuyết xác suất, chứng minh bởi Sergei Bernstein năm 1923. Chúng cũng là trường hợp đặc biệt của bất đẳng thức McDiarmid.
Các bất đẳng thức này cũng đúng khi được chọn không thay thế; trong trường hợp này chúng không còn độc lập. Bài báo của Hoeffding cũng chứa một chứng minh của mệnh đề này. Bài báo của Serfling [2] chứa một chặn trên chặt hơn một chút trong trường hợp lấy mẫu không thay thế.
Bất đẳng thức Markov
Trong lý thuyết xác suất, Bất đẳng thức Markov cho một chặn trên cho xác suất một hàm số không âm của một biến ngẫu nhiên nhận giá trị lớn hơn một hằng số dương. Nó được đặt tên theo nhà toán học Nga Andrey Markov, mặc dù nó đã xuất hiện trong nghiên cứu của Pafnuty Chebyshev (thầy của Markov), và có nhiều nguồn, đặc biệt là trong giải tích, gọi nó là bất đẳng thức Chebyshev hoặc bất đẳng thức Bienaymé.
Bất đẳng thức Markov liên hệ xác suất với giá trị kỳ vọng, và cho một giới hạn (thường không chặt) cho giá trị của hàm phân phối tích lũy của một biến ngẫu nhiên.
Phát biểu
Nếu X là một biến ngẫu nhiên và a > 0, thì
Dưới dạng ngôn ngữ của lý thuyết độ đo, bất đẳng thức Markov khẳng định rằng nếu (X, Σ, μ) là một độ đo, ƒ là một hàm đo được nhận giá trị thực, và , thì
[sửa]Hệ quả: bất đẳng thức Chebyshev
Bất đẳng thức Chebyshev sử dụng phương sai để chặn trên xác suất một biến ngẫu nhiên sai khác nhiều so với giá trị kỳ vọng. Cụ thể là:
với mọi a>0. Ở đây Var(X) là phương sai của X, định nghĩa như sau:
Có thể thu được bất đẳng thức Chebyshev bằng cách áp dụng bất đẳng thức Markov cho biến ngẫu nhiên . Theo bất đẳng thức Markov,






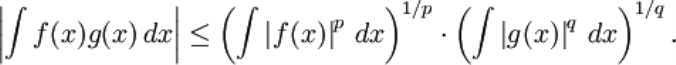
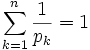

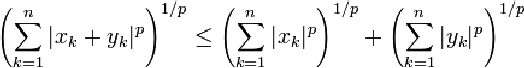
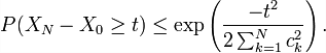
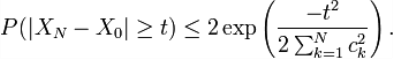
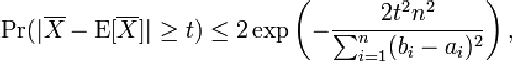


 Trang Trước
Trang Trước



hay quá
ReplyDeletegood
ReplyDeleteThis comment has been removed by the author.
ReplyDeletehay qua
ReplyDeletechả hay tí gì cả
ReplyDeleteHiểu rì đâu mà hay :33
Deletepotoleme có đc gọi là BĐT k
ReplyDeleteCái đó là bất đẳng thức hình học rồi bạn
Deletehay
ReplyDeletek hợp vs thcs xíu náo hết ><
ReplyDeletethpt con k hop><
DeleteĐa phần thôi
Deleteyeah mai thi toán holy yeah boyy
ReplyDeleteDoob đâu ạ
ReplyDelete