Bài 23/a giải tích 1 SGU
Bài 23/a giải và biện luận theo tham số m∈R:
ở đây sẽ giải theo 2 phương pháp Gauss và phương pháp Crammer:
cách 1: dung phương pháp Gauss:
ta có ma trận hệ số:
Với m=0 ta có:
=>Hệ vô nghiệm
Với m=-1 thì (*) trở thành:
Rank=2 hệ vô số nghiệm phụ thuộc 3-2=1 tham số:
Chọn x3=a
Theo phương trình 2 ta được:
X2=3x3-7=3a-7
Thay vào phương trình 1 ta được:
X1=x2+2=3a-7+2=3a-5
Vậy hệ có tập nghiệm là:
(x1,x2,x3)=(3a-5,3a-7,a)
Với m≠0, và m≠-1 ta có:
Với m=1 thì ta được:
Phương trình vô nghiệm.
Với m≠0, m≠1, m≠-1 ta có:
Ta thấy với m≠1 thì hệ có nghiệm duy nhất.
Kết luận: m=0 và m=1 thì hệ vô nghiệm, m=-1 hệ có vô số nghiệm. m≠0, m≠1, m≠-1 hệ có nghiệm duy nhất.
Cách 2 dùng phương pháp Crammer:
Δ=m(m+1)(m-1)
Δ ≠0=>m≠0,m≠1,m≠-1 thì phương trình có nghiệm duy nhất.
Δ=0=>m=0, m=1, m=-1
Với m=0 ta có:
Hê vô nghiệm do phương trình 1 và 2 nghịch nhau:
Với m=1 ta có:
Hệ vô nghiệm do phương trình 2 và 3 nghịch nhau.
Với m=-1 thì ta có:
Hệ vô số nghiệm phụ thuộc 1 tham số.
Kết luận, với m=0 và m=1 thì hệ vô nghiệm, với m=-1 hệ vô số nghiệm, với m=(R/{-1,0,1}) hệ có nghiệm duy nhất.
Có sai sót gì thì comment phía dưới nha. Coppy kí hiệu toán phí dưới và past vào, nếu muốn viết công thức toán.
∆ Δ ∠ ∡ √ ∛ ∜ x² ⁻¹ ∫ π × ∵ ∴ | | , ⊥,∈
∝ ≤ ≥ − ± , ÷ ° ≠ → ∞, ≡ , ≅ , ∑,∪,
¼ , ½ , ¾ , ≈ , [-b ± √(b² - 4ac) ] / 2a
Σ Φ Ω α β γ δ ε η θ λ μ π ρ σ τ φ ω ё й
½ ⅓ ⅔ ¼ ⁰ ¹ ² ⁴ ⁵ ⁶ ⁷ ⁸ ⁹ ⁺ ⁻ ⁼ ⁽ ⁾ ⁿ ₀ ₁ ₂ ₃
₄₅ ₆ ₇ ₈ ₉ ₊ ₋ ₌ ₍ ₎ ∊ ∧ ∏ ∑ ∠ ,∫ ∫ ψ ω Π
∮ ∯ ∰ ∇ ∂ • ⇒ ♠ ★ ✰ ✡ ✪ ✬✫
✭ ✯ ✡ ✸ ✮ ►◄─ ▲ ❶ ❷








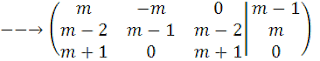
















 Trang Trước
Trang Trước



No comments: