Bài 50: Cho nửa đường tròn (O), đường kính AB=2R. Trên tia đối của tia AB lấy điểm E (EA). Từ E, A, B kẻ các tiếp tuyến với nửa đường tròn. Tiếp tuyến kẻ từ E cắt hai tiếp tuyến kẻ từ A và B theo thứ tự tại C và D.

  a. Gọi M là tiếp điểm của tiếp tuyến kẻ từ E tới nửa đường tròn. Chứng minh tứ giỏc ACMO nội tiếp được trong một đường tròn.

         b. Chứng minh ∆EAC ~ ∆EBD, từ đó suy ra .

         c. Gọi N là giao điểm của AD và BC. Chứng minh MN // BD.

         d. Chứng minh: EA² = EC.EM – EA.AO.

         e. Đặt  = ỏ. Tớnh theo R và ỏ các đoạn AC và BD.

        Chứng tỏ rằng tớch AC.BD chỉ phụ thuộc giỏ trị của R,

        khụng phụ thuộc vào ỏ.

HD:a) ACMO nội tiếp (Dựa vào quĩ tớch cung chứa gúc 90⁰)

       b)  AC // BD (cựng EB) ∆EAC ~ ∆EBD

     (1)mà AC = CM ; BD = MD (T/c hai tiếp tuyến cắt nhau)  (2)

       c) AC // BD (cmt) ∆NAC ~ ∆NBD(3) .Từ 1; 2; 3  MN // BD

        d) =; = mà +++= 180⁰ + = 90⁰ ; + 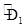= 90⁰ (…)

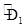   = = = ỏ . Vậy: DB =  = ; Lại cú: AC = OA.tgỏ = R.tgỏ AC.DB = R.tgỏ.

      AC.DB = R² (Đpcm)