=?utf-8?Q?Qui_ho=E1=BA=A1ch_tuy=E1=BA=BFn_t=C3=ADnh=5FDKE31115 ?=
TRƯỜNG ĐẠI HỌC SÀI GÒN ĐỀ THI KẾT THÚC MÔN HỌC
PHÒNG ĐÀO TẠO TẠI CHỨC & TNGV Môn thi: Qui hoạch tuyến tính Lớp: DKE31115
Sinh viên không được tham khảo tài liệu để làm bài
Câu 1. Một xí nghiệp sản xuất ba loại sản phẩm A, B và C bằng ba loại dự trữ D, E và F với số lượng hiện có lần lượt là 60, 80 và 120 đơn vị. Để sản xuất ra mỗi đơn vị sản phẩm A cần sử dụng 2 đơn vị dự trữ D, 6 đơn vị dự trữ E và 1 đơn vị dự trữ F. Các chỉ số đó cho mỗi đơn vị sản phẩm B và C theo thứ tự trên là 4; 0; 2 và 6; 2; 4. Cho biết lợi nhuận thu được trên mỗi đơn vị sản phẩm A, B và C là 4 triệu đồng, 6 triệu đồng và 8 triệu đồng.
1. Hãy thiết lập bài toán qui hoạch tuyến tính nhằm đạt tổng lợi nhuận tối đa và tìm phương án sản xuất tối ưu bằng phương pháp thích hợp.
2. Viết bài toán đối ngẫu của bài toán qui hoạch tuyến tính trên; nêu ý nghĩa kinh tế của bài toan đối ngẫu và tìm phương án tối ưu của nó.
Câu 2. Một công ty có ba xí nghiệp cùng sản xuất một loại sản phẩm. Năng suất trong tháng của ba xí nghiệp lần lượt là  sản phẩm. Hợp đồng công ty phải giao cho bốn nhà phân phối là
sản phẩm. Hợp đồng công ty phải giao cho bốn nhà phân phối là  sản phẩm. Đơn giá (đơn vị tính: 1000 đồng) của mỗi sản phẩm tương ứng với các nhà phân phối được cho bởi ma trận sau:
sản phẩm. Đơn giá (đơn vị tính: 1000 đồng) của mỗi sản phẩm tương ứng với các nhà phân phối được cho bởi ma trận sau:
Hãy tìm kế hoạch phân phối hàng sao cho công ty đạt doanh số lớn nhất.
Đề 01
Câu 1.
1. Gọi  là số đơn vị sản phẩm loại A, B, C cần sản xuất. Ta có mô hình bài toán:
là số đơn vị sản phẩm loại A, B, C cần sản xuất. Ta có mô hình bài toán: 
· Đưa bài toán về dạng chính tắc và bảng đơn hình đầu các bảng trung gian và cuối.
· Dựa vào bảng tối ưu của bài toán 1, ta có  và
và 
Câu 2.
· Kiểm tra điều kiện cân bằng thu phát, ta có 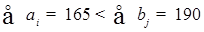 .
.
· Ta thêm một trạm phát giả  và
và  .
.
· Xây dựng phương án ban đầu:
· Kiểm tra tính tối ưu, ta thấy  .
.
· Kiểm tra tính tối ưu, ta thấy  . Ta có phương án tối ưu của bài toán:
. Ta có phương án tối ưu của bài toán:
TRƯỜNG ĐẠI HỌC SÀI GÒN ĐỀ THI KẾT THÚC MÔN HỌC
PHÒNG ĐÀO TẠO TẠI CHỨC & TNGV Môn thi: Qui hoạch tuyến tính Lớp: DKE31115
Sinh viên không được tham khảo tài liệu để làm bài
Câu 1. Một xí nghiệp sản xuất ba loại sản phẩm A, B và C từ ba loại nguyên liệu dự trữ I, II và III với số lượng đơn vị từ các nguyên liệu dự trữ hiện có lần lượt là 120, 80 và 160. Để sản xuất ra mỗi đơn vị sản phẩm loại A cần sử dụng 3 đơn vị nguyên liệu dự trữ loại I, 2 đơn vị nguyên liệu dự trữ loại II và 1 đơn vị nguyên liệu dự trữ loại III. Các số liệu tương tự cho mỗi đơn vị sản phẩm loại B và C lần lượt là 4, 1, 3 và 2, 2, 2. Biết lợi nhuận thu được trên mỗi đơn vị sản phẩm loại A, B và C lần lượt là 2 triệu đồng, 4 triệu đồng và 3 triệu đồng. Anh (chị) hãy
a) Thiết lập bài toán quy hoạch tuyến tính (P) để xí nghiệp sản xuất đạt lợi nhuận tối đa và tìm phương án tối ưu của bài toán;
b) Viết bài toán đối ngẫu (D) của bài toán (P) và tìm phương án tối ưu của nó.
Câu 2. Cho bài toán vận tải có số lượng phát  , số lượng thu
, số lượng thu  và ma trận cước phí
và ma trận cước phí  có dạng sau:
có dạng sau:
a) Giải bài toán vận tải trên;
b) Ngoài phương án tối ưu tìm được ở câu a), bài toán trên còn có phương án tối ưu khác hay không? Nếu có hãy chỉ ra tập phương án tối ưu của nó.
Baøi toaùn ôû daïng chuaån:
F(x) = 2x1 + 3x2 + 4x3 => MAX
Caùc raøng buoäc:
3x1 + 4x2 + 2x3 + x4 = 120
2x1 + x2 + 2x3 + x5 = 80
x1 + 3x2 + 2x3 + x6 = 160
Trong ñoù:
x4, x5, x6 laø bieán phuï
x1 >=0, x2 >=0, x3 >=0, x4 >=0, x5 >=0, x6 >=0
Ci | Xi | Yi | X1 | X2 | X3 | X4 | X5 | X6 | Lamda |
0 | X4 | 120 | 3 | 4 | 2 | 1 | 0 | 0 | 60 |
0 | X5 | 80 | 2 | 1 | 2 | 0 | 1 | 0 | 40 |
0 | X6 | 160 | 1 | 3 | 2 | 0 | 0 | 1 | 80 |
| F(x) | 0 | -2 | -3 | -4 | 0 | 0 | 0 | |
Do coøn toàn taïi giaù trò Delta nhoû hôn 0 neân chöa coù phöông aùn toái öu ta caàn tìm bieán ñöa vaøo
Coät coù giaù trò nhoû nhaát öùng vôùi x3 vaäy bieán ñöa vaøo laø : x3
Haøng coù giaù trò Lamda nhoû nhaát öùng vôùi coät ñoù laø haøng 2
Ci | Xi | Yi | X1 | X2 | X3 | X4 | X5 | X6 | Lamda |
0 | X4 | 40 | 1 | 3 | 0 | 1 | -1 | 0 | 40/3 |
4 | X3 | 40 | 1 | 1/2 | 1 | 0 | 1/2 | 0 | 80 |
0 | X6 | 80 | -1 | 2 | 0 | 0 | -1 | 1 | 40 |
| F(x) | 160 | 2 | -1 | 0 | 0 | 2 | 0 | |
Do coøn toàn taïi giaù trò Delta nhoû hôn 0 neân chöa coù phöông aùn toái öu ta caàn tìm bieán ñöa vaøo
Coät coù giaù trò nhoû nhaát öùng vôùi x2 vaäy bieán ñöa vaøo laø : x2
Haøng coù giaù trò Lamda nhoû nhaát öùng vôùi coät ñoù laø haøng 1
Ci | Xi | Yi | X1 | X2 | X3 | X4 | X5 | X6 | Lamda |
3 | X2 | 40/3 | 1/3 | 1 | 0 | 1/3 | -1/3 | 0 | - |
4 | X3 | 100/3 | 5/6 | 0 | 1 | -1/6 | 2/3 | 0 | - |
0 | X6 | 160/3 | -5/3 | 0 | 0 | -2/3 | -1/3 | 1 | - |
| F(x) | 520/3 | 7/3 | 0 | 0 | 1/3 | 5/3 | 0 | |
Phöông aùn toái öu cuûa baøi toaùn laø : (0,40/3,100/3,0,0,160/3)
Giaù trò haøm muïc tieâu ñaït ñöôïc laø : F(x) = 520/3
Baøi toaùn ôû daïng chuaån:
F(x) = 120x1 + 80x2 + 160x3 + Mx7 + Mx8 + Mx9 => MIN
Caùc raøng buoäc:
3x1 + 2x2 + x3 - x4 = 2
4x1 + x2 + 3x3 - x5 = 3
2x1 + 2x2 + 2x3 - x6 = 4
Phöông aùn toái öu cuûa baøi toaùn môû roäng laø : (1/3,5/3,0,7/3,0,0,0,0,0)
Giaù trò haøm muïc tieâu ñaït ñöôïc laø : F(x) = 520/3
Tags: Đại Học Sài Gòn, Hóa Học hay, Hóa Học Khó, SGU














 Trang Trước
Trang Trước



No comments: