Dao Động Cơ Học - Bài Tập Dạng 1
B. CÁC DẠNG BÀI TẬP
1. Tìm các đại lượng đặc trưng trong dao động điều hòa.
* Các công thức:
+ Li độ (phương trình dao động): x = Acos(wt + j).
+ Vận tốc: v = x' = - wAsin(wt + j) = wAcos(wt + j +  ).
).
+ Gia tốc: a = v' = - w2Acos(wt + j) = - w2x; amax = w2A.
+ Vận tốc v sớm pha  so với li độ x; gia tốc a ngược pha với li độ x (sớm pha
so với li độ x; gia tốc a ngược pha với li độ x (sớm pha  so với vận tốc v).
so với vận tốc v).
+ Liên hệ giữa tần số góc, chu kì và tần số của dao động: w =  = 2pf.
= 2pf.
+ Công thức độc lập: A2 = x2 +  =
= 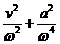 .
.
+ Ở vị trí cân bằng: x = 0 thì |v| = vmax = wA và a = 0.
+ Ở vị trí biên: x = ± A thì v = 0 và |a| = amax = w2A =  .
.
+ Lực kéo về: F = ma = - kx.
+ Quỹ đạo chuyển động của vật dao động điều hòa là một đoạn thẳng có chiều dài L = 2A.
* Phương pháp giải:
+ Để tìm các đại lượng đặc trưng của một dao động điều hòa khi biết phương trình dao động hoặc biết một số đại lượng khác của dao động ta sử dụng các công thức liên quan đến những đại lượng đã biết và đại lượng cần tìm rồi suy ra và tính đại lượng cần tìm theo yêu cầu của bài toán.
+ Để tìm các đại lượng của dao động điều hòa tại một thời điểm t đã cho ta thay giá trị của t vào phương trình liên quan để tính đại lượng đó.
Lưu ý: Hàm sin và hàm cos là hàm tuần hoàn với chu kỳ 2p nên khi thay t vào nếu được góc của hàm sin hoặc hàm cos là một số lớn hơn 2p thì ta bỏ đi của góc đó một số chẵn của p để dễ bấm máy.
+ Để tìm thời điểm mà x, v, a hay F có một giá trị cụ thể nào đó thì ta thay giá trị này vào phương trình liên quan và giải phương trình lượng giác để tìm t.
Lưu ý: Đừng để sót nghiệm: với hàm sin thì lấy thêm góc bù với góc đã tìm được, còn với hàm cos thì lấy thêm góc đối với nó và nhớ hàm sin và hàm cos là hàm tuần hoàn với chu kỳ 2p để đừng bỏ sót các họ nghiệm. Cũng đừng để dư nghiệm: Căn cứ vào dấu của các đại lượng liên quan để loại bớt họ nghiệm không phù hợp.
* Bài tập minh họa:
1. Phương trình dao động của một vật là: x = 6cos(4pt +  ) (cm), với x tính bằng cm, t tính bằng s. Xác định li độ, vận tốc và gia tốc của vật khi t = 0,25 s.
) (cm), với x tính bằng cm, t tính bằng s. Xác định li độ, vận tốc và gia tốc của vật khi t = 0,25 s.
2. Một vật nhỏ khối lượng 100 g dao động điều hòa trên quỹ đạo thẳng dài 20 cm với tần số góc 6 rad/s. Tính vận tốc cực đại và gia tốc cực đại của vật.
3. Một vật dao động điều hoà trên quỹ đạo dài 40 cm. Khi ở vị trí có li độ x = 10 cm vật có vận tốc 20p cm/s. Tính vận tốc và gia tốc cực đại của vật.
cm/s. Tính vận tốc và gia tốc cực đại của vật.
4. Một chất điểm dao động điều hoà với chu kì 0,314 s và biên độ 8 cm. Tính vận tốc của chất điểm khi nó đi qua vị trí cân bằng và khi nó đi qua vị trí có li độ 5 cm.
5. Một chất điểm dao động theo phương trình: x = 2,5cos10t (cm). Vào thời điểm nào thì pha dao động đạt giá trị  ? Lúc ấy li độ, vận tốc, gia tốc của vật bằng bao nhiêu?
? Lúc ấy li độ, vận tốc, gia tốc của vật bằng bao nhiêu?
6. Một vật dao động điều hòa với phương trình: x = 5cos(4pt + p) (cm). Vật đó đi qua vị trí cân bằng theo chiều dương vào những thời điểm nào? Khi đó độ lớn của vận tốc bằng bao nhiêu?
7. Một vật nhỏ có khối lượng m = 50 g, dao động điều hòa với phương trình: x = 20cos(10pt +  ) (cm). Xác định độ lớn và chiều của các véc tơ vận tốc, gia tốc và lực kéo về tại thời điểm t = 0,75T.
) (cm). Xác định độ lớn và chiều của các véc tơ vận tốc, gia tốc và lực kéo về tại thời điểm t = 0,75T.
8. Một vật dao động điều hòa theo phương ngang với biên độ  cm và với chu kì 0,2 s. Tính độ lớn của gia tốc của vật khi nó có vận tốc 10
cm và với chu kì 0,2 s. Tính độ lớn của gia tốc của vật khi nó có vận tốc 10 cm/s.
cm/s.
9. Một vật dao động điều hòa với phương trình: x = 20cos(10pt + 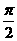 ) (cm). Xác định thời điểm đầu tiên vật đi qua vị trí có li độ x = 5 cm theo chiều ngược chiều với chiều dương kể từ thời điểm t = 0.
) (cm). Xác định thời điểm đầu tiên vật đi qua vị trí có li độ x = 5 cm theo chiều ngược chiều với chiều dương kể từ thời điểm t = 0.
10. Một vật dao động điều hòa với phương trình: x = 4cos(10pt -  ) (cm). Xác định thời điểm gần nhất vận tốc của vật bằng 20p
) (cm). Xác định thời điểm gần nhất vận tốc của vật bằng 20p cm/s và đang tăng kể từ lúc t = 0.
cm/s và đang tăng kể từ lúc t = 0.
* Hướng dẫn giải và đáp số:
1. Khi t = 0,25 s thì x = 6cos(4p.0,25 + ) = 6cos
) = 6cos = - 3
= - 3 (cm);
(cm);
v = - 6.4psin(4pt +  ) = - 6.4psin
) = - 6.4psin = 37,8 (cm/s); a = - w2x = - (4p)2. 3
= 37,8 (cm/s); a = - w2x = - (4p)2. 3 = - 820,5 (cm/s2).
= - 820,5 (cm/s2).
2. Ta có: A =  =
= 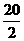 = 10 (cm) = 0,1 (m); vmax = wA = 0,6 m/s; amax = w2A = 3,6 m/s2.
= 10 (cm) = 0,1 (m); vmax = wA = 0,6 m/s; amax = w2A = 3,6 m/s2.
3. Ta có: A =  =
=  = 20 (cm); w =
= 20 (cm); w =  = 2p rad/s; vmax = wA = 2pA = 40p cm/s;
= 2p rad/s; vmax = wA = 2pA = 40p cm/s;
amax = w2A = 800 cm/s2.
4. Ta có: w =  = 20 (rad/s). Khi x = 0 thì v = ± wA = ±160 cm/s.
= 20 (rad/s). Khi x = 0 thì v = ± wA = ±160 cm/s.
Khi x = 5 cm thì v = ± w = ± 125 cm/s.
= ± 125 cm/s.
5. Ta có: 10t =  ð t =
ð t =  (s). Khi đó x = Acos
(s). Khi đó x = Acos = 1,25 (cm); v = - wAsin
= 1,25 (cm); v = - wAsin = - 21,65 (cm/s);
= - 21,65 (cm/s);
a = - w2x = - 125 cm/s2.
6. Khi đi qua vị trí cân bằng thì x = 0 ð cos(4pt + p) = 0 = cos(± ). Vì v > 0 nên 4pt + p = -
). Vì v > 0 nên 4pt + p = -  + 2kp
+ 2kp
ð t = -  + 0,5k với k Î Z. Khi đó |v| = vmax = wA = 62,8 cm/s.
+ 0,5k với k Î Z. Khi đó |v| = vmax = wA = 62,8 cm/s.
7. Khi t = 0,75T =  = 0,15 s thì x = 20cos(10p.0,15 +
= 0,15 s thì x = 20cos(10p.0,15 +  ) = 20cos2p = 20 cm;
) = 20cos2p = 20 cm;
v = - wAsin2p = 0; a = - w2x = - 200 m/s2; F = - kx = - mw2x = - 10 N; a và F đều có giá trị âm nên gia tốc và lực kéo về đều hướng ngược với chiều dương của trục tọa độ.
8. Ta có: w =  = 10p rad/s; A2 = x2 +
= 10p rad/s; A2 = x2 +  =
=  ð |a| =
ð |a| =  = 10 m/s2.
= 10 m/s2.
9. Ta có: x = 5 = 20cos(10pt +  ) ð cos(10pt +
) ð cos(10pt +  ) = 0,25 = cos(±0,42p).
) = 0,25 = cos(±0,42p).
Vì v < 0 nên 10pt +  = 0,42p + 2kp ð t = - 0,008 + 0,2k; với k Î Z. Nghiệm dương nhỏ nhất trong họ nghiệm này (ứng với k = 1) là 0,192 s.
= 0,42p + 2kp ð t = - 0,008 + 0,2k; với k Î Z. Nghiệm dương nhỏ nhất trong họ nghiệm này (ứng với k = 1) là 0,192 s.
10. Ta có: v = x' = - 40psin(10pt -  ) = 40pcos(10pt +
) = 40pcos(10pt +  ) = 20p
) = 20p
ð cos(10pt +  ) =
) =  = cos(±
= cos(± ). Vì v đang tăng nên: 10pt +
). Vì v đang tăng nên: 10pt +  = -
= - + 2kp
+ 2kp
 + 0,2k. Với k Î Z. Nghiệm dương nhỏ nhất trong họ nghiệm này là t =
+ 0,2k. Với k Î Z. Nghiệm dương nhỏ nhất trong họ nghiệm này là t =  s.
s.Tags: Dao Động Cơ Học, Tài Liệu Ôn Thi Đại Học, vật lý, VatLy

 Trang Trước
Trang Trước





No comments: