Động Hóa Học 3
5. Các phản ứng phức tạp.
Các phản ứng đơn giản chỉ là những trường hợp may mắn ngẫu nhiên, trong thực tế chủ yếu là các phản ứng phức tạp (nhiều giai đoạn).
Hai tiên đề:
1. Qui tắc độc lập. Nếu trong hệ đồng thời xảy ra nhiều phản ứng thì mỗi phản ứng đều tuân theo Định luật tác dụng khối lượng và độc lập với nhau. Khi đó sự biến thiên chung của hệ bằng tổng biến thiên gây ra bởi từng phản ứng.
2. Giai đoạn quyết định tốc độ phản ứng.
Khi phản ứng nhiều giai đoạn nối tiếp thì tốc độ chung của phản ứng được quyết định bởi tốc độ của giai đoạn chậm nhất.
5.1. Phản ứng thuận nghịch n = 1
A 
B
t = 0 a b
t = t a - x b + x
t = ¥ a - xc b + xc
-
= k1[A] - k2 [B]
hoặc -
= k1(a - x) - k2 (b + x) (1)
Þ 
= k1(a - x) - k2 (b + x) = (k1 + k2) 
Đặt 
= A (2)
Þ 
= 
(k1 + k2) dt
- ln 
= - [ln (A - x) - lnA] = (k1 + k2)t
Þ ln 
= (k1 + k2)t Þ (k1 + k2) = 
ln
(3)
Cần tìm A: lấy A : k1
: k1 ® 
(Lưu ý: 
= A và 
= K)
Þ 
= A (4)
* Phản ứng đạt cân bằng khi W1 = W2 Þ 
= 0 (biến thiên nồng độ A = B = const)
Þ k1 (a - xC) - k2 (b + xC) = 0 Þ K = 
= 
(5)
Như vậy ta có hệ phương trình:
(k1 + k2) = 
ln
K = 
= 
Trong đó theo (4) A = 
Biết xC 
tính được K 
A 
(k1 + k2) 
k1,k2
Ví dụ: D-Menton 
L-menton
NH4CNS 
(NH2)2CS
Tiocyanat Tiourê
CH2OH-(CH2)2-COOH 
+ H2O
g-oxibutyric axit g -lacton
a = 18,23; b = 0; xC = 13,28
Các số liệu thực nghiệm:
| t, pt | x | k1 + k2 | t, pt | x | k1 + k2 |
| 21 | 2,41 | 0,0355 | 160 | 10,35 | 0,0382 |
| 50 | 4,96 | 0,0374 | 220 | 11,55 | 0,0370 |
| 100 | 8,11 | 0,0384 | ¥ | 13,28 | 0,0373 |
| 120 | 8,10 | 0,0377 |
|
|
|
Lời giải:
Þ K = 
= 
= 
= 0,3727
Dựng đồ thị lg(A - x) - t hoặc lg 
- t, xác định được:
Þ k1 + k2 = 0,037; 
= 0,3727
Þ k1 = 0,0271 và k2 = 0,0102 (ph-1)
5.2. Phản ứng thuận nghịch bậc 2
A + B 
C + D
CH3COOH + C2H5 
CH3COOC2H5 + H2O
-
= k1[A] [B] - k2 [C] [D]
Þ 
= k1(a - x) (b - x) - k2 (c + x) (d + x)
Điều kiện đơn giản nhất: a = b ; c = d = 0
Þ 
= k1(a - x)2 - k2 x2 (1)
Þ 
= (k1 - k2) 
(2)
= (k1 - k2) (m1 - x) (m2 - x) (3)
trong đó m1, m2 = nghiệm của phương trình: x2 - 2
x + 
= 0
hay x2 - 
x + 
Þ m1,2 = 
(4)
Từ (3) lấy 
k1 - k2 = 
ln 
(5)
5.3. Các phản ứng song song.
HNO3 + phenol ¾®
Sơ đồ:
Phản ứng 1: 
= k1 (a - x) (*)
Phản ứng 2: 
= k2 (a - x) (**) x = x1 + x2
Tốc độ chung: 
= 
+ 
= k1 (a - x) + k2 (a - x)
Þ 
= (k1 + k2) (a - x) (1)
Þ (k1 + k2) = 
ln 
(2)
Þ k = 
ln
Nếu số phản ứng song song là n thì: 
= 
ln
Tương tự với phản ứng n = 2: A + B
Nếu a ¹ b:
(k1 + k2) = 
ln 
(3)
Chia (*) cho (**): Þ 
= 
® k2dx1 = k1dx2 ® lấy tích phân 
Þ 
= 
= const ® Biết [B] [C] ® tìm được k1, k2.
Nếu có 3 phản ứng: k1 + k2 + k3 = k; 
= const1; 
= const2
5.4. Phản ứng nối tiếp
Ví dụ: xà phòng hoá TG
TG + NaOH ¾® DG + RCOONa
DG + NaOH ¾® MG + RCOONa
MG + NaOH ¾® G + RCOONa
Sơ đồ: A 
B 
C
t = 0 a
t = t a - x x - y y
Tốc độ chuyển hoá A: 
= k1 (a - x) (1)
Þ (a - x) = a. 
(2)
x = (a - a. 
)
Tốc độ chuyển hoá B: B hình thành do phản ứng 1 và mất đi bởi phản ứng 2 nên
= k1 (a - x) - k2 (x - y) (3)
Thay (2) vào (3): 
= k1 a. 
- k2 (x - y) (4)
Þ 
+ k2 (x - y) = k1 a. 
(5)
Giải phương trình vi phân bậc 1 (5):
Đặt (x - y) = z ® 
+ k2z = k1 a. 
(6)
Giả sử k1a. 
= 0 ® 
+ k2z = 0 (7)
Þ 
= - k2 dt (8)
Lấy tích phân (nguyên hàm)
lnz = -k2t + ln E ® z = E. 
(9)
Vì vế phải của (6) ¹ 0 và là hàm của t nên E = f(t). Lấy vi phân (9) theo t:
= -k2 E. 
+ 
(10)
Đưa (9) và (10) vào (6) ta có:
- k2 E. 
+ 
+ k2 E. 
= k1 a. 
(11)
k2z
Þ 
= 
® dE = 
dt (12)
Lấy tích phân của (12): E = 
a. 
+ C (13)
Đặt (13) vào (9) ta có: z = 
a. 
+ C.
(14)
Nếu t = 0 ® z = 0 ® C = -
(15)
Đặt (15) vào (14), thay z = x - y ta có:
x - y = a
- a
(16)
Hoặc x - y = a
(
-
) (17)
Đặt giá trị x ở (2) vào (17): y = (a - a
) - a
(
-
) (18)
Hoặc: y = a 
+ 
(19)
Biểu diễn các hàm pt. 2, pt. 17, pt.19 ứng với nồng độ của nồng độ A, B, C tương ứng theo thời gian ta có hình ....
Cực đại B = y - x xuất hiện ở tm ứng với 
= 0 (20)
Lấy vi phân biểu thức (x - y) (pt 17):
= a 
(-k1
+ k2
) (21)
Đặt bằng không ta có: k1.
= k2. 
(22)
Logarit hoá ta có: lnk1 – k1tm = lnk2 – k2tm
Þ lnk1 – lnk2 = k1tm – k2tm = tm (k1– k2)
Þ tm = 
= 
(23)
Đặt 
= r ® k2 = (1/r)k1 (24)
Thay (24) vào (23): tmax = 
(25)
Thay tmax ở pt. (25) vào (x - y) ở pt. (17):
Þ (x - y)max = 
(26)
Như vậy lượng cực đại của [B] (hay x - y) không phụ thuộc vào W1, W2 mà phụ thuộc vào tỉ lệ k1/k2 = r. Nếu k1/k2 càng lớn thì (x - y)max càng lớn, tmax càng gần gốc toạ độ.
Điểm uốn S ứng với tmax: ở đây tốc độ tạo C là max.
Nếu k1 << k2 thì sau 1 thời gian phản ứng: 
<< 
Vậy (x - y) ở (17) trở thành: (x - y) = 
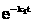(27)
Mặt khác từ pt. (2): a.
= a - x
Vậy: (x - y) = 
(28)
Hoặc: 
= 
(29)
Như vậy, tỉ số lượng chất B/A = const sau một thời gian tức là tốc độ giảm A (sinh ra B) và giảm B như nhau. Đây là trạng thái giả ổn định, khi đó [B] = constant.
Nếu k1 << k2 thì 
, khi đó 
và y ở pt. (19) có dạng:
y = a(1 - 
) (30)
Đây là phương trình phản ứng bậc 1 đơn giản.
Trang Trước
No comments: