ỨNG DỤNG PHƯƠNG PHÁP HOÁ PHÓNG XẠ TRONG PHÂN TÍCH
II. ỨNG DỤNG PHƯƠNG PHÁP HOÁ PHÓNG XẠ TRONG PHÂN TÍCH
Bài tập 1. Tính thời gian bán huỷ của các nuclit có thời gian bán huỷ quá dài, khi mà việc xác định thời gian bán huỷ gặp khó khăn do sự thay đổi hoạt độ phóng xạ không thể đo được bằng thực nghiệm.
Ví dụ: Trong 1kg urani ở cân bằng phóng xạ có chứa 0,34mg 226Ra có
t1/2 = 1600 năm. Có thể tính được thời gian bán huỷ của 238U:
Bài tập 2. Tính hàm lượng của các nuclit nằm trong cân bằng phóng xạ của một dãy.
trong đó M1, M2 là nguyên tử lượng.
Ví dụ: Tính lượng 228Ra có t1/2(2) là 5,75 năm có trong 1g 232Th có t1/2(1) là 1,41.1010 năm:
Những tính toán như vậy có tầm quan trọng lớn trong công nghệ xử lý quặng urani và thori, nó cung cấp thông tin về lượng bã thải phóng xạ cần được xử lý và quản lý.
Bài tập 3.Xác định hàm lượng đồng vị mẹ trong khoáng vật thông qua đo hoạt độ phóng xạ của nuclit con.
Công thức tính khối lượng của nuclit mẹ từ hoạt độ phóng xạ của nuclit con có thể rút ra trực tiếp từ các phương trình (2.10) và (2.34):
Để xác định hàm lượng urani trong quặng người ta có thể tiến hành đo hoạt độ của Th-234 hoặc Pa-234m.
Hàm lượng rađi trong mẫu có thể được xác định với độ nhạy rất cao nhờ đo rađon nằm ở cân bằng phóng xạ với rađi.
Bài tập 4. Phương pháp đánh dấu bằng đồng vị phóng xạ trong phân tích
Để xác định hàm lượng axit aspatic trong sản phẩm thuỷ phân một protein, người ta thêm vào dung dich thuỷ phân 5,0 mg axit aspatic đánh dấu có hoạt độ phóng xạ riêng 0,46 mCi/mg. Sau đó, người ta tách ra 0,21 mg axit aspatic nguyên chất có hoạt độ phóng xạ riêng 0,01 mCi/mg. Tính lượng axit aspatic có trong mẫu dung dịch thuỷ phân ban đầu.
Chú thích: Axit aspatic là một amino axit có trong cơ thể động thực vật, có nhiều trong mật mía, củ cải đường, công thức phân tử C4H7NO4.
Giải :
Gọi x là khối lượng axit aspatic (mg) có trong dung dịch thuỷ phân,
y là lương axit (đánh dấu) đưa thêm vào,
D là hoạt độ phóng xạ,
As1 là họat độ phóng xạ riêng của chất đánh dấu ban đầu,
As2 là hoạt độ dung dịch sau khi đánh dấu, ta có:
As1 = D/y (1)
As2 = D/(x+y) (2).
Chia (1) cho (2) và biến đổi một cách đơn giản:
x = y(As1/ As2 - 1). (3)
Thay số vào (3), thu được: x = 225 mg
III. ĐỊNH TUỔI BẰNG PHƯƠNG PHÁP PHÓNG XẠ
1. TÍNH t KHI CÓ N0/N
Bài tập 1. .
Khi nghiên cứu một mẫu cổ vật nguồn gốc hữu cơ chứa 1 mg C, người ta thấy rằng tỉ lệ đồng vị 14C/12C của mẫu là 1,2 x 10-14.
a. Có bao nhiêu nguyên tử 14C có trong mẫu?
b. Tốc độ phân rã của 14C trong mẫu bằng bao nhiêu?
c. Tuổi của mẫu nghiên cứu bằng bao nhiêu?
Cho t1/2(14C) = 5730 năm, hoạt độ phóng xạ riêng của cacbon thời chưa có các hoạt động hạt nhân của con người là 227 Bq/kgC.
Giải
147N + 10n ® 126C + 31H. Phản ứng có thể viết tóm tắt: 14N(n,t)12C
(nơtron nhanh)
147N + 10n ® 146C + 11p. Phản ứng có thể viết tóm tắt: 14N(n,p)14C
(nơtron nhiệt)
a. Tổng số nguyên tử C trong mẫu cổ vật = (10-3g/12g/ngtg) x 6,02 x 1023 ngt/ngtg = 5,02 x 1019 ngt
Số nguyên tử 14C là N »(1,2 x 10-14)(5,02 x 1019) = 6,02 x 105 ngt.
b. A = (ln2/5730 x 365 x 24 x 3600 s) x 6,02 x 105 = 2,3 x 10-6 Bq
c. tuổi t = [ln(227 x 10-6/2,3 x 10-6)]/(ln2)/5730 năm = 38 000 năm
2. TÍNH t KHI CÓ Dt/Pt
Khi không có thông tin về N0 việc định tuổi sẽ tính theo tỉ số Dt/Pt
Trong đó Dt là số hạt nhân ở thời điểm t của một đồng vị con cháu bền,
Pt là số hạt nhân của mẹ ở thời điểm t.
Con không có mặt khi t = 0 và không mất đi (do khuếch tán, bay hơi...)
Dt + Pt = P0 (1)
Pt = P0 e-lt (2)
Chia 2 vế cho Pt ;
Dt/ Pt + 1 = elt (3)
Bài tập
Hãy tính tuổi của loại đá có tỉ số nguyên tử 206Pb so với 238U bằng 0,60. Cho t1/2 của 238U là 4,5.109 năm.
 = [1/(ln2/4,5.109 năm)].ln(1 + 0,6) = 3,1.109 năm
= [1/(ln2/4,5.109 năm)].ln(1 + 0,6) = 3,1.109 năm
2.2. Trường hợp đồng vị con có mặt tại t = o
Dt + Pt = P0 + D0 (5)
Để định được tuổi trong trường hợp này cần có thông tin về một đồng vị bền khác của con mà đồng vị này không được tạo ra do phân rã của mẹ.
Dst = Dso = Ds (6)
Chia cả 2 vế của (5) cho Ds :
Dt/ Ds + Pt/ Ds = D0/ Ds + P0/ Ds (7)
Hay:
Dt/ Ds = D0/ Ds + P0/ Ds - Pt/ Ds (8)
Thay P0 = Pt elt (9)
Ta có:
Dt/ Ds = D0/ Ds + ( elt - 1) ( Pt/ Ds) (10)
y = b + ax (11)
Có thể vẽ đường thẳng y = b + ax và thu được hệ số góc là ( elt - 1). Cũng có thể tính a khi có 2 cặp giá trị của y và x.
Bài tập
Tuổi của đá mặt trăng, do tầu Apollo 16 thu lượm đựơc, được xác định dựa vào tỉ số nguyên tử của các đồng vị 87Rb/87Sr và 87Sr/86Sr trong một số khoáng vật có trong mẫu:
| Khoáng vật | 87Rb/86Sr | 87Sr/86Sr |
| A | 0,004 | 0,699 |
| B | 0.180 | 0,709 |
a) 87Rb phóng xạ b- . Hãy viết phương trình biểu diễn quá trình phân rã hạt nhân này. t1/2(87Rb) = 4,8.1010 năm.
b) Tính tuổi của mẫu đá. Biết rằng 87Sr và 86Sr là các đồng vị bền và ban đầu (t = 0) tỉ số 87Sr/86Sr trong các khoáng A và B là như nhau.
Giải:
3787Rb ® 3887Sr + b-
Phương trình (10) có thể viết như sau:
87Srnow/86Sr = 87Sr0/86Sr + (elt - 1) 87Rbnow/86Sr (12)
Trong mẫu A:
0,699 = 87Sr0/86Sr + (elt -1)0,004 (a)
Trong B:
0,709 = 87Sr0/86Sr + (elt - 1)0,180 (b)
(b) - (a) và biến đổi ta có:
elt = (0,709 – 0,699)/(0,180 – 0,004) +1 = 1,0568
® lt = (ln2)t/t1/2 = ln1,0568
t = (4,8.1010.ln1,0568)/ln2 = 3,8.109 năm
Trong bài tập trên người ta có thể đòi tính thêm 87Sr0/86Sr ở t = 0.
Người ta có thể cho các giá trị khác nhau của 87Rb/86Sr và 87Sr/86Sr trong nhiều khoáng vật khác nhau. Nếu đưa lên đồ thị mà thu được một đường thẳng thì đó là bằng chứng cho thấy ở t = 0, tỉ số 87Sr0/86Sr trong các khoáng này như nhau.
Có khi người ta cho biết tuổi khoáng vật (t), để tính l hoặc t1/2.
Người ta thường định tuổi dựa vào phân rã 40K thành 40Ar (phép định tuổi K/Ar) hoặc 235U và 207Pb; 238U và 206Pb.
3. MỘT SỐ DẠNG BÀI TẬP KHÁC
Bài tập 1.
Cho dãy phóng xạ sau:
Giả thiết rằng ban đầu chỉ có một mình radon trong mẫu nghiên cứu với hoạt độ phóng xạ 3,7.104 Bq,
a) Viết các phương trình biểu diễn các phân rã phóng xạ trong dãy trên.
b) Tại t = 240 min (phút) hoạt độ phóng xạ của 222Rn bằng bao nhiêu?
c) Cũng tại t = 240 min hoạt độ phóng xạ của 218Po bằng bao nhiêu?
d) Tại t = 240 min hoạt độ phóng xạ chung lớn hơn, nhỏ hơn hay bằng hoạt độ phóng xạ ban đầu của 222Rn.
Lời giải bài tập 6
a)
22286Rn ® 21884Po + 42He
21884Po ® 21482Pb + 42He
21482Pb ® 21483Bi + b-
21483Bi ® 21484Po + b-
21484Po ® 21082Pb + a
3,7.104 Bq = 1mCi , 240 min = 4 h
b) A1 = A01e-lt = 1mCi.e-ln2.4/24.3,82 = 0,97 mCi
c) t = 240 min > 10 t1/2(Po), hệ đã đạt được cân bằng phóng xạ và
+ Quan niệm gần đúng rằng có cân bằng thế kỉ (l1<<l2) nên:
A2 = A1 = 0,97 mCi
+ Thật ra cân bằng là tạm thời nên
A1/A2 = 1 – t1/2(2)/t1/2(1) ® A2 = A1/[1 – 3,1/(3,82.24.60)] = 0,9702 mCi
d) A = A1 + A2 + ...> A01
BÀI TẬP 1:
1. Dưới tác động của nơtron năng lượng cao trong tia vũ trụ, hạt nhân Nitơ-14 biến đổi thành hạt nhân C-12 cùng với sự tạo thành hạt nhân triti. Hãy viết phương trình của phản ứng hạt nhân nói trên. 2. Dưới tác động của nơtron nhiệt trong tia vũ trụ, hạt nhân Nitơ-14 biến đổi thành hạt nhân C-14 cùng với sự tạo thành hạt nhân 1H. Hãy viết phương trình của phản ứng hạt nhân nói trên. 14N(n,p)14C
Giải
147N + 10n ® 126C + 31H. Phản ứng có thể viết tóm tắt: 14N(n,t)12C
147N + 10n ® 146C + 11p. Phản ứng có thể viết tóm tắt: 14N(n,p)14C
Bài tập 2.
1. Viết phương trình biểu diễn sự phân rã b- của hạt nhân triti.
2. Viết phương trình của các quá trình phân rã phóng xạ:
3. Viết phương trình của các quá trình phân rã phóng xạ sau:
Phân rã b- của Sr-90 Phân rã a của Th-232
Phân rã b+ của Cu-62 Phân rã b- của C-14
4. Chuỗi phân rã của U-238 kết thúc ở Pb-206. Trong chuỗi này phải có bao nhiêu phân rã a và bao nhiêu phân rã b-?
Giải
1. 31H ® 32He + b-
2.
22286Rn ® 21884Po + 42He
21884Po ® 21482Pb + 42He
21482Pb ® 21483Bi + b-
21483Bi ® 21484Po + b-
21484Po ® 21082Pb + a
3.
9038Sr ® 9039Y + b-
23290Th ® 22888Ra + 42He
6229Cu ® 6228Ni + b+
146C ® 147N + b-
4. 8 phân rã a và 6 phân rã b-
Bài tập 3. Thời gian bán huỷ của triti 3H t1/2(3H) = 12,33 năm). Một mẫu triti có hoạt độ phóng xạ 1 MBq.
- Đổi hoạt độ phóng xạ nói trên ra Ci,
- Tính số nguyên tử và khối lượng triti của mẫu,
- Tính hoạt độ phóng xạ riêng của triti
Giải
106/3,7x1010 » 27mCi
N = A/l = A/ (0,693/t1/2) = 106/s /(0,693/ 12, 33 x 24x3600 x 365 s) = 5,59 x 1014 nguyên tử.
M = N/6,02 x 1023 = 2,78 x 10 -9 g
As = (106/s)/(2,78 x 10 -9 g)
Bài tập 4
Thời gian bán huỷ của 14C là t1/2(14C) = 5730 năm. 2 gam một mẫu chứa 14C có hoạt độ phóng xạ 3,7 Bq.
- Đổi hoạt độ phóng xạ nói trên ra Ci,
- Tính số nguyên tử 14C có trong mẫu,
- Tính hoạt độ phóng xạ riêng của mẫu .
Giải
3,7 Bq = 3,7 /3,7 x 1010 Ci = 10-10 Ci.
N = A x t1/2/0,693 = 3,7 x 5730 x 365 x 24 x 3600/0,6935 = 9,64 x 1011 hạt nhân.
As = 3,7 Bq /2g = 1,85 Bq/g
Bài tập 9
Cacbon 14 được tạo thành từ nitơ do tác dụng của các nơtron (chậm) trong các tia vũ trụ, rồi đi vào cơ thể sinh vật qua quang hợp và lưu chuyển thực phẩm của động thực vật. 14C phân rã b- với thời gian bán huỷ t1/2 = 5730 năm. Sự phân tích cacbon phóng xạ trong các cơ thể sống cho giá trị hoạt độ phóng xạ riêng của cacbon là
230 Bq/kg cacbon.
a). Viết các phương trình phản ứng hạt nhân biểu diễn quá trình hình thành và phân rã của 14C trong tự nhiên.
b) Tỉ lệ đồng vị 14C/12C trong cơ thể sống bằng bao nhiêu?
c) Một nhà khảo cổ lấy được một mẫu, được cho là của một hoá thạch hữu cơ, tại một kim tự tháp ở Ai-cập và thấy rằng tỉ lệ đồng vị của cacbon trong mẫu này, xác định bằng phương pháp khối phổ, là 14C/12C = 6. 10-13 . Ông sẽ cho rằng tuổi của mẫu nói trên là bao nhiêu?
Giải
1.

3. Hoạt độ 230 Bq/kg tương ứng với tỉ số đồng vị 14C/12C sau đây:
(khi bỏ qua hàm lượng của 13C). Trong đó, w là tỉ số đồng vị 14C/12C
Chú ý: Khi thay số cần đổi 230 Bq/kg ra 230/1000 (Bq/g), vì mol nguyên tử tính ra gam.
Vì 6.0×10–13 / 1.20×10–12 = 1/2, một khoảng thời gian bằng thời gian bán huỷ đã trôi qua (chúng ta sử dụng giá trị thời gian bán huỷ 5730 năm để xác định tuổi). Nhà khảo cổ học cho rằng chất bột này đã được làm ra vào năm 3560 trước CN.
4. Thực ra, nhóm phenoxyacetyl được hình thành từ axit phenoxyacetic được tổng hợp trong công nghiệp từ các sản phẩm chế biến than và dầu mỏ. Nó không chứa cacbon phóng xạ. Chỉ có 8 trong số 16 nguyên tử cacbon là có nguồn gốc tự nhiên (tạo thành từ cơ thể sống). Như thế, trong phần có nguồn gốc tự nhiên, hàm lượng 14C phải gấp đôi w = 1.2×10–12, nghĩa là chất bột này là sản phẩm của thời nay.
Bài tập 11.
1. Khi phân tích quặng urani (uranium) người ta tìm thấy 3 đồng vị của urani là 238U, 235U và 234U, đều có tính phóng xạ. Hai đồng vị 235U và 234U có phải là đồng vị con cháu của 238U không? Tại sao? (Người ta quan sát được ở các nguyên tố phóng xạ tự nhiên tính phóng xạ a và tính phóng xạ b).
2. Khi thuỷ luyện một mẫu quặng urani lấy từ mỏ Nông Sơn (Quảng Nam), người ta thu được dung dịch có nồng độ UO2SO4 (uranyl sunfat) là 0,01M còn nồng độ Fe2(SO4)3 lên tới 0,05M. Sự tách urani khỏi sắt và các tạp chất khác có thể thực hiện bằng phương pháp chiết hoặc trao đổi ion, nhưng cũng có thể bằng kết tủa phân đoạn.
Có thể kết tủa 99% lượng sắt (Fe3+) có trong dung dịch nói trên ở pH bằng bao nhiêu mà không làm mất lượng urani có mặt trong dung dịch? Giả định rằng sự hấp phụ urani trên bề mặt kết tủa Fe(OH)3 là không đáng kể. Biết rằng trong điều kiện nhiệt độ tiến hành thí nghiệm, tích số tan của UO2(OH)2 là 10-22 của Fe(OH)3 là 3,8.10-38.
3. Nước thải của dung dịch thuỷ luyện quặng urani có chứa đồng vị phóng xạ 226Ra có thời gian bán huỷ 1600 năm. Để bảo vệ môi trường, người ta có thể đồng kết tủa rađi với BaSO4 và lưu giữ khối chất thải này trong kho thải hạt nhân. Cần lưu giữ chừng bao lâu để hoạt độ phóng xạ của khối chất thải này chỉ còn lại <1/1000 hoạt độ ban đầu?
4. Người ta có thể tinh chế urani, thu được từ thuỷ luyện quặng, bằng phương pháp chiết với pha hữu cơ là tributylphotphat (viết tắt là TBP) được pha loãng với dầu hoả. Dung dịch đưa vào tinh chế là dung dịch nước của UO2(NO3)2 (uranyl nitrat). Để xây dựng đường đẳng nhiệt chiết của uranyl nitrat, người ta có thể làm n thí nghiệm với dung dịch nước có nồng độ uranyl nitrat trước khi chiết là Co (chẳng hạn chọn Co khoảng bằng nửa nồng độ của dung dịch uranyl nitrat bão hoà), thể tích pha hữu cơ không đổi là V, còn thể tích pha nước trong các thí nghiệm từ 1, 2 đến n thay đổi từ 1V, 2V đến nV. Pha nước và pha hữu cơ được đưa vào phễu chiết, lắc cho đến khi đạt đến cân bằng, tức là khi nồng độ urani trong hai pha không thay đổi nữa, rồi tách riêng hai pha (nước, hữu cơ) để xác định các nồng độ urani x1, x2, x3 ,..., xn trong pha nước và y1 , y2, y3...,yn. trong pha hữu cơ. Trong hệ chiết nói trên không xẩy ra sự liên hợp phân tử của UO2(NO3)2 trong pha hữu cơ.
a. Hãy biểu diễn các giá trị y1, y2,..., yn qua Co và x1, x2,..., xn.
b. ở các Co nhỏ so với độ tan bão hoà của uranyl nitrat trong nước, hệ số phân bố D = yn/xn có thể chấp nhận là không đổi. Hãy chọn trong các dãy bất đẳng thức dưới đây một trường hợp đúng và giải thích lý do của sự lựa chọn:
A. x1<x2<x3 và y1<y2<y3
B. x1>x2>x3 và y1>y2>y3
C. x1<x2<x3 và y1>y2>y3
D. x1<x2<x3 và y1>y2>y3
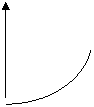
c. Đường đẳng nhiệt chiết của uranyl nitrat được vẽ bằng cách đặt các giá trị x trên trục hoành, y trên trục tung, bao gồm cả các giá trị ứng với n lớn. Đồ thị nào dưới đây có dạng của đường đẳng nhiệt chiết?
A B C D
d. Hãy đề nghị một phương án để chiết được > 95% lượng urani có trong 100ml dung dịch nước vào 100 ml pha hữu cơ. Nồng độ uranyl nitrat trong nước và thành phần hệ dung môi chiết cho phép chấp nhận hệ số phân bố D không đổi và bằng 6.
Giải
1. Khi xảy ra phân rã b, nguyên tử khối không thay đổi. Khi xảy ra 1 phân rã a, nguyên tử khối thay đổi 4 đ.v. khối lượng nguyên tử (u). Như thế, số khối của các đồng vị con cháu phải khác số khối của đồng vị mẹ 4n(u), với n là số nguyên. Chỉ 234U thoả mãn điều kiện này với n = 1. Trong 2 đồng vị 234U, 235U, chỉ 234U là đồng vị con cháu của 238U.
Nồng độ Fe3+ còn lại trong dung dịch sau khi 99% sắt trong dung dịch Fe2(SO4)3 0,05 M bị kết tủa là:
[Fe3+] = 2.0,05.10-2 M = 10-3 M.
[OH-] cần có trong dung dịch để [Fe3+] chỉ còn lại trong dung dịch với nồng độ10-3 M là:
[OH-] = (38)1/3.10-12 ứng với giá trị pH là:
pH = -log{10-14/(38)1/3.10-12} = 2 + (1/3)log38 = 2,53.
ở pH đó, tích số ion của UO2(OH)2 trong dung dịch 0,01M là:
[UO22+][OH-]2 = 0,01.[(38)1/3.10-12]2 = 1,13.10-25< 10-22
Vì tích số ion nói trên rất nhỏ so với tích số tan của UO2(OH)2 (TUO2(OH)2) nên urani không kết tủa trong điều kiện trên.
3.
a. Sau n chu kì bán huỷ của rađi, hoạt độ phóng xạ của thùng chất thải chỉ còn lại 1/2n. Hoạt độ phóng xạ chỉ còn <1/1000 khi:
2n > 103 hay:
nlog2 > 3. Rút ra: n > 3/0,301» 10. Thời gian cần lưu giữ để hoạt độ phóng xạ của khối chất thải rađi còn <1/1000 là : t ³ 10x1600 năm = 16 000 năm.
4.
a.
|
| TN1 | TN2 | TN3 |
| TNn |
| X | x1 | x2 | x3 | ... | xn |
| Y | y1 = Co-x1 | y2=2(Co-x2) | y3=3(Co-x3) |
| yn=n(Co-xn) |
b.
Từ biểu thức trên rút ra:
(2)
Lấy đạo hàm xn theo n, ta có:
(xn)' = CoD/(D + n)2 > 0 (3)
Như thế , xn tăng khi n tăng: x1 < x2 < x3. (4)
y1 = x1.D ; y2 = x2.D ; y3 = x3.D
Từ các bất đẳng thức (4) rút ra: y1 < y2 < y3 . (5)
A. x1<x2<x3 và y1<y2<y3 A là đáp án đúng
B. x1>x2>x3 và y1>y2>y3 sai
C. x1<x2<x3 và y1>y2>y3 sai
D. x1<x2<x3 và y1>y2>y3 sai
c. Khi n tăng, nồng độ uranyl nitrat trong pha nước và pha hữu cơ nằm cân bằng, xn và yn, đều tăng dần lên. Nhưng yn không thể vượt qua nồng độ bão hoà của uranyl nitrat trong pha hữu cơ. Vì thế đường đằng nhiệt chiết sẽ tiệm cận với đường thẳng nằm ngang
y = ybh (ybh là nồng độ bão hoà uranyl nitrat trong pha hữu cơ). Chỉ có đồ thị A có dáng điệu như vậy.
d. Nếu chiết 1 lần thì nồng độ uranyl nitrat trong pha nước sau khi chiết được tính như sau
D = y/x = (C0 - x)/x (6)
Rút ra: x/ C0 = 1/ (D+1) = 1 / 7 = 0,143 > 0,1
Như thế lượng uranyl nitrat còn lại trong dung dịch nước sẽ lớn hơn 10% nồng độ ban đầu.
Để chiết được > 95% urani vào pha hữu cơ ta có thể chia 100 ml dung môi chiết thành n phần bằng nhau, rồi chiết thành n bậc. Dung dịch nước sau khi chiết với phần dung môi thứ nhất ( bậc chiết 1), tiếp tục đưa vào chiết với phần dung môi thứ 2 (bậc chiết 2)...cứ thế cho đến bậc n.
Khi 100 ml dung môi hữu cơ được chia thành n phần bằng nhau, tỉ lệ thể tích pha nước (Vaq) với thể tích pha hữu cơ (Vo) trong mỗi bậc chiết sẽ là:
Vaq/Vo = 100 ml/ (100 ml/n) = n
Biểu thức của hệ số phân bố cho bậc chiết 1 sẽ là:
D = y1/x1 = n(C0 - x1)/x1 (7)
Rút ra: x1 = n C0 / (D+n) = C0/[(D/n) +1] (8)
Vào bậc chiết thứ 2, nồng độ ban đầu của pha nước là x1. Tương tự như biểu thức (7) ta có:
x2 = x1 / [(D/n) +1] (9).
Thay x1 bằng biểu thức (8) ta thu được:
x2 = C0 / [(D/n) +1] 2 (10)
Tương tự như vậy, với bậc chiết thứ 3,..., thứ n ta có:
x3 = C0 / [(D/n) +1] 3 (11)
xn = C0 / [(D/n) +1] n (12)
Để > 95% urani được chiết vào pha hữu cơ thì:
xn/C0 = 1 / [(D/n) +1] n < 5x10-2 (13)
Lập bảng biến thiên 1 / [(D/n) +1] n theo n:
n = 1 2 3
1/[(D/n) +1] n = 1/7 > 5.10-2 1/16 > 5.10-2 1/27 < 5.10-2
Kết luận: Có thể chia 100 ml dung môi hữu cơ thành 3 phần bằng nhau và chiết 3 bậc để đưa được > 95% urani vào pha hữu cơ.
Chú ý: Phần d còn có thể giải theo nhiều cách khác nhau. Các cách giải đúng khác đều được cho đủ điểm. Các học sinh đặc biệt giỏi có thể đưa ra phương án chiết liên tục ngược dòng và tính số bậc lí thuyết. Có học sinh làm theo phương án loại trừ dần (thử phương án chiết 2 bậc, rồi sang phương án chiết 3 bậc...). Để tính n từ phương trình (13), học sinh có thể logarit hoá ...






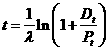
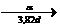
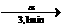




















 Trang Trước
Trang Trước



No comments: