Bài 1. Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại

H và cắt đường tròn (O) lần lượt tại M,N,P.

Chứng minh rằng:

1. Tứ giác CEHD, nội tiếp .
2. Bốn điểm B,C,E,F cùng nằm trên một đường tròn.
3. AE.AC = AH.AD; AD.BC = BE.AC.
4. H và M đối xứng nhau qua BC.
5. Xác định tâm đường tròn nội tiếp tam giác DEF.

Lời giải: 

1.      Xét tứ giác CEHD ta có:

= 90⁰ ( Vì BE là đường cao)

= 90⁰ ( Vì AD là đường cao)

=>   +  = 180⁰

Mà    và   là hai góc đối của tứ giác CEHD , Do đó  CEHD là tứ giác nội tiếp

2.      Theo giả thiết: BE là đường cao => BE ^ AC => = 90⁰.

CF là đường cao => CF ^ AB => = 90⁰.

Như vậy E và F cùng nhìn BC dưới một góc 90⁰ => E và F cùng nằm trên đường tròn  đường kính BC.

Vậy bốn điểm B,C,E,F cùng nằm trên một đường tròn.

3.      Xét hai tam giác  AEH và ADC ta có: =   = 90⁰ ; Â là góc chung

=> D AEH ~ DADC =>  => AE.AC = AH.AD.

* Xét hai tam giác  BEC và ADC ta có: = = 90⁰ ; 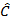là góc chung

=> D BEC ~ DADC =>  => AD.BC = BE.AC.

4. Ta có 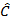₁ = ₁ ( vì cùng phụ với góc ABC)

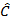₂ = ₁ ( vì là hai góc nội tiếp cùng chắn cung BM)

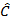=> ₁ = 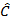 ₂ => CB là tia phân giác của góc HCM; lại có CB ^ HM => D CHM cân tại C

=> CB còng là đương trung trực của HM  vậy H và M đối xứng nhau qua BC.

5. Theo chứng minh trên bốn điểm B,C,E,F cùng nằm trên một đường tròn

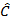=> ₁ = ₁ ( vì là hai góc nội tiếp cùng chắn cung BF)

Còng theo chứng minh trên CEHD là tứ giác nội tiếp

ü 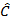 ₁ = ₂ ( vì là hai góc nội tiếp cùng chắn cung HD)

ü  ₁ = ₂ => EB là tia phân giác của góc FED.

Chứng minh tương tự ta còn có FC là tia phân giác của góc DFE mà BE và CF cắt nhau tại H do đó H là tâm đường tròn  nội tiếp tam giác  DEF.