Đáp Án ToPo
Câu 1: Giả sử X là một T2- không gian thì mọi tập hợp compact trong X đều là tập hợp đóng.
Chứng minh: Giả sử X là T2 không gian và F là tập compact của X. Ta sẽ chứng minh X\F la tập mở.
Lấy với mọi và một điểm tùy ý  . Vì x ≠ y và X là T2 không gian nên tồn tại các lân cận mở Vy của y và Ux(y) của x sao cho Vy
. Vì x ≠ y và X là T2 không gian nên tồn tại các lân cận mở Vy của y và Ux(y) của x sao cho Vy  Ux(y)=
Ux(y)= . Hiễn nhiên
. Hiễn nhiên  là một phủ mở của F. Vì F compact nên
là một phủ mở của F. Vì F compact nên  có chứa phủ con hữu hạn
có chứa phủ con hữu hạn  . Đặt
. Đặt  và
và  . ta có
. ta có  và U là một lân cận của x.
và U là một lân cận của x.  và
và  với
với  nên
nên  với
với  . Do đó
. Do đó 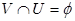 nghĩa là
nghĩa là  . Vì vậy X\F là một lân cận của
. Vì vậy X\F là một lân cận của  và X\F là tập hợp mở.
và X\F là tập hợp mở.
Câu 2: Cho không gian mêtric (X,d) là đầy đủ. Giả sử dãy (Fn) là dãy giảm các tập con đóng khác rỗng của X và  . Chứng minh
. Chứng minh  .
.
Với mọi n, Fn khác rỗng nên ta chọn được xn thuộc Fn. Dãy (xn)n thuộc Fn ta sẽ chứng minh dãy này là dãy Côsi.
Lấy  bất kỳ. Do
bất kỳ. Do  nên tồn tại n0≥1 sao cho
nên tồn tại n0≥1 sao cho  . Vì
. Vì  với mọi k=1,2,… nên với mọi p,q≥n0 thì xp,xq thuộc Fn0 do đó
với mọi k=1,2,… nên với mọi p,q≥n0 thì xp,xq thuộc Fn0 do đó  suy ra (xn)n là dãy Côsi trong X mà X đầy đủ nên
suy ra (xn)n là dãy Côsi trong X mà X đầy đủ nên  .
.
Với mọi n cố định, và số tự nhiên k có  nên
nên  với mọi k. Từ đó
với mọi k. Từ đó  là một dãy trong Fn với mọi n. Do
là một dãy trong Fn với mọi n. Do  là dãy con của
là dãy con của  nên xn+k cũng hội tụ đến x. Do Fn đóng nên x thuộc Fn.Vì n tùy ý nên
nên xn+k cũng hội tụ đến x. Do Fn đóng nên x thuộc Fn.Vì n tùy ý nên  . vậy
. vậy 
Câu 3:
Giả sử E là một tập con tùy ý của không gian tôpô X. Xét hàm đặc trưng  từ X vào đường thẳng thực. chứng minh rằng lên tục tại p thuộc X khi và chỉ khi p không là điểm biên của E.
từ X vào đường thẳng thực. chứng minh rằng lên tục tại p thuộc X khi và chỉ khi p không là điểm biên của E.
Chứng minh: giả sử  khi và chỉ khi với mọi lân cận W của x đều có
khi và chỉ khi với mọi lân cận W của x đều có  . Do đó
. Do đó  . Ta có
. Ta có  là hai lân cận rời nhau của 0 và1 trong
là hai lân cận rời nhau của 0 và1 trong  .
.
Như vậy  khi và chỉ khi tồn tại lân cận V của
khi và chỉ khi tồn tại lân cận V của  sao cho mọi lân cận W của x thỏa
sao cho mọi lân cận W của x thỏa  . Do đó
. Do đó  không liên tục tại x.
không liên tục tại x.
Câu 4: giả sử X là một tập hợp khác rỗng bất kỳ. Đặt
a) Chứng minh rằng T là một tôpô trên X.
Ta kiểm tra 3 tiên đề
T1)  theo định nghĩa;
theo định nghĩa;  vì
vì  hữu hạn.
hữu hạn.
T2) giả sử  là một họ tùy ý các tập thuộc T ta sẽ chứng minh
là một họ tùy ý các tập thuộc T ta sẽ chứng minh 
Nếu  thì tồn tại i0 sao cho
thì tồn tại i0 sao cho  . Lúc đó
. Lúc đó  nhưng do
nhưng do  nên
nên  cũng hữu hạn. do đó G thuộc T.
cũng hữu hạn. do đó G thuộc T.
T3) Giả sử  . Đặt
. Đặt  . Nếu
. Nếu  thì G thuộc T.
thì G thuộc T.
Vậy T là một tôpô trên X.
b) Điều kiện cần và đủ để T là tôpô rời rạc là tập X vô hạn.
c) Chứng minh rằng X là không gian compact, thỏa tiên đề tách T1.
Tags: Đại Học Sài Gòn, SGU






 Trang Trước
Trang Trước



Còn phần tiếp theo ko ạ
ReplyDelete