ĐỀ CƯƠNG ÔN TẬP HỌC KÌ I - toán 9
ĐỀ CƯƠNG ÔN TẬP HỌC KÌ I (2010_2011)
I. Lý thuyết:
A. Phần Đại Số:
I-Định nghĩa tính chất căn bậc hai:
a) Với a ³ 0 số được gọi là căn bậc hai số học(CBHSH) của a. x =
được gọi là căn bậc hai số học(CBHSH) của a. x = Û
Û 
b) + Mỗi số dương a có hai căn bậc hai là hai số đối nhau:  >0 và -
>0 và - < 0
< 0
+ Số 0 có căn bậc hai duy nhất là 0. Số âm không có căn bậc hai .
c) Với hai số a và b không âm, ta có: 0 ≤ a < b Û 
II-Các công thức biến đổi căn thức
3.  (Với A ³ 0; B ³ 0) 4.
(Với A ³ 0; B ³ 0) 4.  (Với B ³ 0)
(Với B ³ 0)
5.  (Với A ³ 0; B ³ 0); 6.
(Với A ³ 0; B ³ 0); 6. (Với A < 0; B ³ 0)
(Với A < 0; B ³ 0)
7.  (Với AB ³ 0; B ¹ 0) 8.
(Với AB ³ 0; B ¹ 0) 8.  (Với B > 0)
(Với B > 0)
9. (Với A ³ 0; A¹B2 ) 10.
(Với A ³ 0; A¹B2 ) 10. (Với A,B ³ 0;và A¹B )
(Với A,B ³ 0;và A¹B )
III-Hàm số bậc nhất
1)Định nghĩa:Hàm số bậc nhất là hàm số được cho bởi coâng thức:y = ax + b.(a, b là các số cho trước và a ¹ 0 ).
2) Các tính chất của hàm số bậc nhất y = ax + b (a ¹ 0 ) :
+ Hàm số bậc nhất y = ax + b xác định với mọi giaù trị xÎ R.
+ Hàm số đồng biến trên R khi a > 0 và nghịch biến trên R Khi a < 0.
3) Đồ thị của hàm số y = ax + b (a¹ 0): Là một đường thẳng:
- Cắt trục tung tại điểm có tung độ bằng b
- Song song với đường thẳng y = ax nếu b ¹ 0; trùng với đương thẳng y = ax nếu b = 0
Chuù yù : b = 0  ñồ thị của hàm số y = ax (a¹ 0) là một đường thẳng qua goác toïa ñoä
ñồ thị của hàm số y = ax (a¹ 0) là một đường thẳng qua goác toïa ñoä
4) Vị trí tương đối của hai đường thẳng:
- Cho hai đường thẳng: (D) y= ax + b và (D') y= a'x + b' (a và a' là hệ số goùc)
* (D) cắt (D') Û a ¹ a'; * (D) º (D')  * (D)// (D')
* (D)// (D')  ;
;
*(D) cắt (D') taïi ñieåm thuoäc truïc tung 
5) Cách tìm giao điểm của đồ thị y = ax+ b với các trục toạ độ:
+ Giao với trục tung : cho x = 0 Þ y = b Þ A(0; b)
+ Giao với trục hoành: cho y = 0 Þ x = -b/a Þ B(-b/a; 0)
6) Cách tính góc a tạo bởi đường thẳng(D): y= ax +b với trục Ox
*Khi a > 0 ta có a góc nhoïn naèm phía treân Ox Chuù yù :Tính toaùn kieåm tra laïi 
*Khi a < 0 ta có a góc tuø naèm phía treân Ox Chuù yù :Tính toaùn kieåm tra laïi , với
, với 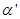 là góc kề bù với gocù
là góc kề bù với gocù tạo bởi (D) với trục Ox
tạo bởi (D) với trục Ox
B. Phần Hình học:
I/ Các hệ thức về cạnh và đường cao trong tam giác vuông.

 Cho DABC vuông tại A, đường cao AH
Cho DABC vuông tại A, đường cao AH
1 ) AC2 = BC. HC; AB2 = BC. BH
2) AH 2 = HB. HC
3) AH.BC = AB.AC
II/ Tỉ số lượng giác của góc nhọn
a) Định nghĩa các tỉ số lượng giác của goùc nhọn ( 00 <a <900)
Sin a =  ; Cos a =
; Cos a = ; Tan a =
; Tan a =  ; Cot a =
; Cot a = 

b) Một số tính chất của các tỉ số lượng giác:
* Cho góc nhọn a. Ta có: 0 < Sina <1; 0< Cosa <1;
*Coâng thöùc cô baûn : Sin2a + Cos2a=1; tana =  ; cota =
; cota =  ; tana.cota = 1
; tana.cota = 1
c) Các hệ thức về cạnh và góc trong tam giác vuông::
b = a.sinB; c = a.sinC (Caïnh goùc vuoâng = Cạnh huyền nhân với sin góc đối)
b = a.cosC; c = a.cosB (Caïnh goùc vuoâng = Cạnh huyền nhân với cos góc kề)
b = c.tanB; c = b.tanC (Caïnh goùc vuoâng = Cạnh góc vuông kia nhân tan góc đối)
b = c.cotC; c = b.cotB (Caïnh goùc vuoâng = Cạnh góc vuông kia nhân cot góc kề)
d)Bảng lượng giaùc của một số góc đặc biệt:
Góc a Tỉ số lượng giỏc | 00 | 300 | 450 | 600 | 900 |
sin a | 0 | 1 | |||
cos a | 1 | 0 | |||
tan a | 0 | 1 | |||
cot a | 1 | 0 |
III/Định nghĩa đường tròn:
Tập hợp (quỹ tích) các điểm cách điểm 0 cho trước một khoảng không đổi R> 0 là đường tròn tâm O bán kính R.
IV/ Quan hệ đường kính dây cung.
1/Định lí1: "Đường kính là dây cung lớn nhất của đường tròn"
2/ Định lí2: Trong một đường tròn đường kính vuông góc với dây cung thì qua trung đieåm cuûa dây cung ấy
3-/Định lí 3:Đường kính đi qua trung điểm của một dây cung không đi qua tâm thì vuông góc với dây đó.
V/ Định lý liên hệ giữa dây và khoảng cách đến tâm
* Trong một đường tròn.:
+ Hai dây bằng nhau thì cách đều tâm và hai dây cách đều tâm thì bằng nhau
+ Dây lớn hơn thì gần tâm hơn và dây gần tâm hơn thì lớn hơn.
VI/ Vị trí tương đối của đường thẳng và (O;R) với d là khoảng cách từ tâm O đến đường thẳng.
STT | VỊ TRÍ TƯƠNG ĐỐI | SỐ ĐIỂM CHUNG | HỆ THỨC LIEN HỆ |
1 | Đường thẳng và đường tròn cắt nhau | 2 | d < R |
2 | Đường thẳng tiếp xúc với đường tròn | 1 | d = R |
3 | Đường thẳng và đường tròn không giao nhau | 0 | d > R |
VII/Tiếp tuyến và tính chất của tiếp tuyến:
 1/ Định nghĩa: Một đường thẳng gọi là 1 tiếp tuyến của đường tròn nếu nó chỉ có một điểm chung với đường tròn đó.
1/ Định nghĩa: Một đường thẳng gọi là 1 tiếp tuyến của đường tròn nếu nó chỉ có một điểm chung với đường tròn đó.
2/ Dấu hiệu nhận biết tiếp tuyến của đường tròn.
 3 /Tính chất hai tiếp tuyến cắt nhau.
3 /Tính chất hai tiếp tuyến cắt nhau.
AB và AC là hai tiếp tuyến của (O)
II. Bài tập:
Đại số
· Căn thức bậc hai:
I/ Thực hiện phép tính:
II/ Rút gọn biểu thức:
a/ Tìm điều kiện của x để A có nghĩa b/ Rút gọn biểu thức A c/ Tính giá trị A với 
a/ Rút gọn B b/ Tính giá trị B khi 
a/ Tìm x để C có nghĩa b/ Rút gọn biểu thức C c/ T ìm x để C = 3
a/ Tìm x để E có nghĩa b/ rút gọn E c/ Tìm x để E > 0
a/ Rút gọn biểu thức G b/ Tìm x để G = 2
6. Rút gọn biểu thức sau
a/ Trục căn thức ở mẫu của A,B và C b/ Tính A – B + 6C
III/ Giải phương trình:
· Hàm số bậc nhất:
a/ Tìm m để hàm số đồng biến,nghịch biến
b/Tìm m để đồ thị hàm số đi qua điểm  . Vẽ đồ thị hàm số với m vừa tìm được.
. Vẽ đồ thị hàm số với m vừa tìm được.
c/ Bằng đồ thị xác định tọa độ giao của đường thẳng vừa vẽ với đường thẳng 
a/X ác định m đường thẳng (D) đi qua góc tọa độ.
b/ Tìm m để đường thẳng (D) đi qua A(3;4).Vẽ đồ thị với m vừa tìm được
c/ Bằng đồ thị xác định tọa độ xác định tọa độ giao điểm của đường thẳng (D) với đường thẳng
a/ Vẽ (D) và (D')
b/ Bằng đồ thị xác định tọa độ giao điểm của (D) và (D')
a/Nêu tính chất của hai hàm số trên và vẽ đồ thị.
b/Xác định tọa độ giao điểm của hai đường thẳng trên và thử lại bằng phép phương pháp đại số.
Hình học:
Baøi 1:Cho M  ñöôøng trung tröïc cuûa ñoaïn OM caét (O) taïi A vaø B , caét OM taïi H
ñöôøng trung tröïc cuûa ñoaïn OM caét (O) taïi A vaø B , caét OM taïi H
a) Chöùng minh : H laø trung ñieåm cuûa AB vaø ΔOAM ñeàu
b)Veõ hai tieáp tuyeán taïi A vaø B cuûa (O) ,chuùng caét nhau taïi C. Chöùng minh :O,M ,C thaúng haøng.Tính AC , AH theo R
c)Ñöôøng thaúng vuoâng goùc vôùi OA taïi O caét BC taïi N .Chöùng minh:MN laø tieáp tuyeán cuûa (O) vaø M laø taâm ñöôøng troøn noäi tieáp ΔABC
d)Goïi I laø giao ñieåm cuûa AB vaø ON .Chöùng minh:HI.HB + HO.HC = R2
Baøi 2: Cho nöûa ñöôøng troøn (O;R), ñöôøng kính AB. Keû tieáp tuyeán Ax, By vôùi ñöôøng troøn. Laáy ñieåm M baát kì treân nöûa ñöôøng troøn, keû tieáùp tuyeán taïi M vôùi ñöôøng troøn , noù caét Ax taïi C vaø caét By taïi D.
a/ Chöùng minh:  vaø CD = AC + BD
vaø CD = AC + BD
b/ AD caét BC taïi N. Chöùng minh: MN // AC
c/ MN caét AB taïi H. Chöùng minh: N laø trung ñieåm MH
d/ Goïi r laø baùn kính ñöôøng troøn taâm I noäi tieáp D MAB.
Chöùng minh: SMAB =  , vaø tính baùn kính r , bieát
, vaø tính baùn kính r , bieát  ?
?
Baøi 3: Cho (O;R) .Töø moät ñieåm A ngoaøi ñöôøng troøn (O) veõ caùc tieáp AB,AC ñeán ñöôøng troøn (B,C) laø tieáp ñieåm. Ñoaïn thaúng AO caét (O) taïi I; CD laø ñöôøng kính cuûa ñöôøng troøn (O).
a) Chöùng minh AO ^ BC vaø BD || AO
b)Chöùng minh I laø taâm ñöôøng troøn noäi tieáp tam giaùc ABC.
c)Goïi K laø trung ñieåm cuûa AO.
Chöùng minh K laø taâm ñöôøng troøn ngoaïi tieáp D ABC.
ÑEÀ KIEÅM TRA HOÏC KYØ I – QUAÄN I – (06 – 07)
Baøi 1 : Tính : a)  +
+  - 2
- 2 +
+  b)
b)  -
-  c)
c)  -
-
Baøi 2 : Cho haøm soá y = - x coù ñoà thò laø (d1) vaø haøm soá y = 2x - 3 coù ñoà thò laø (d2)
x coù ñoà thò laø (d1) vaø haøm soá y = 2x - 3 coù ñoà thò laø (d2)
a) Veõ (d1) vaø (d2) treân cuøng maét phaúng toïa ñoä
b) Xaùc ñònh caùc heõ soá a, b bieát ñöôøng thaúng (d3) y = ax + b song song vôùi (d1) vaø ñi qua ñieåm A(-2; 1)
Baøi 3 : Cho bieåu thöùc A = ( -
- ):
): (vôùi x>0, x
(vôùi x>0, x 1)
1)
a) Ruùt goïn bieåu thöùc A
b) Tìm x ñeå A = -2
Baøi 4 : Cho ñöôøng troøn (O;R) ñöôøng kính AB vaø ñieåm C thuoäc ñöôøng troøn (O) ( C khaùc A vaø B). veõ OH vuoâng goùc vôùi daây AC taïi H
a) Chöùng minh H laø trung ñieåm cuûa AC vaø OH// BC
b) Tieáp tuyeán taïi C cuûa (O) caét tia OH taïi D. Chöùng minh ñöôøng thaúng DA laø tieáp tuyeán taïi A cuûa ñöôøng troøn (O)
d) Tìm vò trí cuûa ñieåm C treân (O) sao cho SACD =  SABC.
SABC.
ÑEÀ KIEÅM TRA HOÏC KYØ I – QUAÄN I – (07 – 08)
Baøi 1 : Tính : a)  .(
.( - 3
- 3 ) b)
) b)  +
+  c)
c)  +
+
Baøi 2 : Ruùt goïn bieåu thöùc : A = ( -
-  ).(1 -
).(1 -  ) (vôùi x>0, x
) (vôùi x>0, x 1)
1)
Baøi 3 : Cho haøm soá y = 2x coù ñoà thò laø (d1) vaø haøm soá y = - x + 3 coù ñoà thò laø (d2)
x + 3 coù ñoà thò laø (d2)
a) Veõ (d1) vaø (d2) treân cuøng maét phaúng toïa ñoä
b) Xaùc ñònh caùc heõ soá a, b bieát ñöôøng thaúng (d3) y = ax + b song song vôùi (d1) vaø caét (d2) taïi moät ñieåm coù hoøanh ñoä baèng 4.
Baøi 4 : Cho ñöôøng troøn (O;R) ñöôøng kính AB. Laáy ñieåm H naèm giöõa hai ñieåm A vaø O. Veõ daây cung CD vuoâng goùc vôùi AB taïi H.
a) Chöùng minh H laø trung ñieåm cuûa CD vaø tính  ACB
ACB
b) Goïi E laø ñieåm ñoái xöùng vôùi A qua H. Chöùng minh töù giaùc ACED laø hình thoi, suy DE vuoâng goùc vôùi BC taïi F
c) Chöùng minh HF laø tieáp tuyeán cuûa ñöôøng troøn (I) ñöôøng kính EB
d) Tìm vò trí cuûa H treân ñoïan OA sao cho tam giaùc BCD ñeàu vaø tính SBCD theo R.
ÑEÀ KIEÅM TRA HOÏC KYØ I _ QUAÄN I _Naêm hoïc 2008-2009
Baøi 1 (2 ñieåm) Tính : a) b)
b) c)
c)
Baøi 2 : (1.5 ñieåm) a)Giaûi phöông trình:
Baøi 3 : (1.5 ñieåm) Cho haøm soá  coù ñoà thò (d1) vaø haøm soá
coù ñoà thò (d1) vaø haøm soá  coù ñoà thò (d2).
coù ñoà thò (d2).
a)Veõ (d1) vaø (d2) treân cuøng maët phaúng toaï ñoä.
b)Xaùc ñònh caùc heä soá a ,b bieát ñöôøng thaúng (d3) : y = ax +b song song vôùi (d1) vaø caét (d2) taïi ñieåm thuoäc truïc tung
Baøi 4 : (1 ñieåm) Cho bieåu thöùc  (vôùi x > 0 vaø x ≠ 4 )
(vôùi x > 0 vaø x ≠ 4 )
a) Ruùt goïn bieåu thöùc
b) Tìm giaù trò nguyeân cuûa x ñeå A nhaän giaù trò nguyeân
Baøi 5:(4ñieåm) Cho ñöôøng troøn (O; R) ñöôøng kính AB .Laáy ñieåm M baát kyø treân (O) ( M≠A ; M ≠ B ) Tieáp tuyeán taïi M caét hai tieáp tuyeán taïi A vaø B theo thöù töï taïi C vaø D
a) Chöùng minh : CD = AC + BD vaø 
b) Tính tích CA.DB theo R
c) Ñöôøng troøn ñöôøng kính OM caét OC ,OD laàn löôït taïi E vaø F .Chöùng minh E laø trung ñieåm cuûa ñoaïn thaúng MA
d) Goïi N laø giao ñieåm cuûa AF vaø BE .Cho goùc MAB = 3 goùc MBA.Tính dieän tích  theo R
theo R
Tags: THCS Nguyễn Du, Toán Lớp 9





















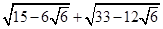




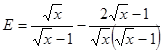













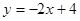






 Trang Trước
Trang Trước





No comments: