Chöông IV. BAÁT PHÖÔNG TRÌNH BAÄC NHAÁT MOÄT AÅN

§1. LIEÂN HEÄ GIÖÕA THÖÙ TÖÏ VAØ PHEÙP COÄNG.
LIEÂN HEÄ GIÖÕA THÖÙ TÖÏ VAØ PHEÙP NHAÂN

A/ KIEÁN THÖÙC VAØ KÓ NAÊNG CAÀN NHÔÙ

I. Lieân heä giöõa thöù töï vaø pheùp coäng :

1. Baát ñaúng thöùc : Ta goïi heä thöùc daïng a < b (hay a > b, a £ b, a ³ b) laø baát ñaúng thöùc vaø goïi a laø veá traùi, b laø veá phaûi cuûa baát ñaúng thöùc.

Ta goïi heä thöùc daïng a < b (hay a > b, a £ b, a ³ b) laø baát ñaúng thöùc vaø goïi a laø veá traùi, b laø veá phaûi cuûa baát ñaúng thöùc.

2. Lieân heä giöõa thöù töï vaø pheùp coäng

Tính chaát. Khi coäng cuøng moät soá vaøo caû hai veá cuûa moät baát ñaúng thöùc ta ñöôïc baát ñaúng thöùc môùi cuøng chieàu vôùi baát ñaúng thöùc ñaõ cho.

II. Lieân heä giöõa thöù töï vaø pheùp nhaân

1. Lieân heä giöõa thöù töï vaø pheùp nhaân vôùi soá döông

Tính chaát : Khi nhaân caû hai veá cuûa moät baát ñaúng thöùc vôùi cuøng moät soá döông ta ñöôïc baát ñaúng thöùc môùi cuøng chieàu vôùi baát ñaúng thöùc ñaõ cho.

2. Lieân heä giöõa thöù töï vaø pheùp nhaân vôùi soá aâm

Tính chaát : Khi nhaân caû hai soá cuûa moät baát ñaúng thöùc vôùi cuøng moät soá aâm ta ñöôïc baát ñaúng thöùc môùi ngöôïc chieàu vôùi baát ñaúng thöùc ñaõ cho.

3. Tính chaát baéc caàu cuûa thöù töï : Vôùi ba soá a, b, c ta coù: neáu a < b vaø b < c thì a < c.

B/ BAØI TAÄP :

& BAØI TAÄP CÔ BAÛN

91. Cho x > y, haõy so saùnh :

a) x + 2009 vaø y + 2009                b) x – 2010 vaø y – 2010                     c) x + y vaø 2y

92. Haõy so saùnh m vaø n neáu :

a) m + 2009 ³ n + 2009                 b) m – 2009 £ n – 2009.

93. Cho x £ y, haõy so saùnh :

a) 2009x vaø 2009y                         b) 69x – 7 vaø 69y – 7

c) –60x vaø –60y                             d) –75x + 8 vaø –75y + 8.

94. Cho m > n. Chöùng minh raèng :

a) m + 2009 > n + 2007                 b) 8m – 5 > 8n – 5                              c) 9m + 2 > 9n – 1.

95. Chöùng minh :

a) 20(–11) + 2009 < 20(–10) + 2009                    b) (–30)4 + 75 < (–30) (–4) + 75

96. Cho a < b. chöùng minh :

a) 8a + 5 < 8b + 5                                                  b) –9a – 34 > –9b – 34.

97. So saùnh m vaø n neáu :

a) m + 4 ³ n + 4                                                     b) –6m £ –6n

c) 5m – 8 > 5n – 8                                                 d) –2m – 7 < –2n – 7.

98. Cho p > q, haõy so saùnh :

a) –3000p vaø –3000q                    b) 500p – 9 vaø 500q – 9                     c) 45p + 96 vaø 45q + 95.

99. So saùnh soá x vaø soá 0 neáu :

a) 7x < 9x                                       b) 8x < 7x                               c) –5x > –9x.

& BAØI TAÄP TRAÉC NGHIEÄM

100. Choïn caâu traû lôøi ñuùng :

Xeùt caùc khaúng ñònh sau : (I) x – 472 ³ y – 472 neáu x ³ y ; (II) x ³ y neáu x – 472 ³ y – 472.

A. Chæ coù (I) ñuùng                                                             B. Chæ coù (II) ñuùng

C. Caû (I) vaø (II) ñuùng                                           D. Caû (I) vaø (II) sai.

& BAØI TAÄP NAÂNG CAO

101. Chöùng minh raèng :

a) a² + b² ³ 2ab                                          b) (a + b)² ³ 4ab                     c) 2(a² + b²) ³ (a + b)²

d) (ax + by)² £ (a² + b²) (x² + y²)              e) a² + b² + c² + d² + e² ³ a(b + c + d + e)

f) a² + b² + c² ³ ab + bc + ca.

102. Cho a, b, c > 0. Chöùng minh raèng :

a)  ³ 2                                              b) a³ + b³ ³ a²b + ab²              c)  ³ a + b + c

d)  ³ a + b + c                       e)

f)  £ 3(a + b + c).

103. Cho a, b, c laø ñoä daøi ba caïnh cuûa moät tam giaùc. Chöùng minh raèng :

a) a² + b² + c² < 2(ab + bc + ca)                            b) (a + b + c)(a – b + c)(–a + b + c) £ abc

& BAØI THI CHOÏN HOÏC SINH GIOÛI TOAÙN

104. a) Chöùng minh caùc baát ñaúng thöùc sau :

1) (a² + b²)(a² + 1) ³ 4a²b, vôùi moïi a, b.              2) , vôùi moïi a, b > 0

3)  

(Ñeà thi choïn HSG Toaùn 8, Tröôøng THCS Hoa Lö, Quaän 9 – TP. Hoà Chí Minh, naêm hoïc 2000 – 2001)

b) 1) Chöùng minh baát ñaúng thöùc : a² + b² + c² ³ ab + bc + ac

2) Cho a, b, c laø ba soá döông. Chöùng minh :  

(Ñeà thi choïn HSG Toaùn 8, Tröôøng Nguyeãn Du, Quaän 1 – TP. Hoà Chí Minh, naêm hoïc 2001 – 2002)

c) Cho a ³ b ³ c > 0. Chöùng minh baát ñaúng thöùc :  

(Ñeà thi choïn hoïc sinh gioûi Toaùn lôùp 8, Quaän 6 – TP. Hoà Chí Minh, naêm hoïc 1998 – 1999)

105. a) Cho ba soá a, b, c sao cho : 0 £ a £ 2, 0 £ b £ 2, 0 £ c £ 2 vaø a + b + c = 3.

Chöùng minh raèng a² + b² + c² £ 5

(Ñeà thi choïn hoïc sinh gioûi Toaùn lôùp 8, Quaän 6 – TP. Hoà Chí Minh, naêm hoïc 1998 – 1999)

b) Cho x, y laø soá döông thoaû maõn x³ + y⁴ £ x² + y³. Chöùng minh raèng :

       1. x³ + y³ £ x² + y²                             

2. x² + y³ £ x + y²

(Ñeà thi choïn hoïc sinh gioûi Toaùn lôùp 9, Quaän 1 – TP. Hoà Chí Minh, naêm hoïc 2004 – 2005)

c) Cho a³ + b³ = 2. Chöùng minh raèng 0 < a + b £ 2.

(Ñeà thi vaøo lôùp 10 chuyeân Toaùn,Tröôøng THPT chuyeân Leâ Hoàng Phong,TP.HCM, naêm hoïc 2008 – 2009)

§2. BAÁT PHÖÔNG TRÌNH MOÄT AÅN. BAÁT PHÖÔNG TRÌNH BAÄC NHAÁT MOÄT AÅN

A/ KIEÁN THÖÙC VAØ KÓ NAÊNG CAÀN NHÔÙ

I. Baát phöông trình baäc nhaát moät aån

1. Môû ñaàu

– Ta goïi heä thöùc 16x + 5 ³ 70 (1) laø moät baát phöông trình vôùi aån laø x; trong ñoù 16x + 5 laø veá traùi vaø 70 laø veá phaûi cuûa baát phöông trình.

– Khi thay giaù trò x = 5 vaøo (1), ta ñöôïc: 16.5 + 5 ³ 70 laø khaúng ñònh ñuùng. Ta noùi soá 5 (hay giaù trò x = 5) laø moät nghieäm cuûa baát phöông trình (1).

– Khi thay x = 2 vaøo (1), ta ñöôïc: 16.2 + 5 ³ 75 laø khaúng ñònh sai. Ta noùi soá 2 (hay giaù trò x = 2) khoâng phaûi laø nghieäm cuûa baát phöông trình (1).

2. Taäp nghieäm cuûa baát phöông trình

– Taäp hôïp taát caû caùc nghieäm cuûa moät baát phöông trình ñöôïc goïi laø taäp nghieäm cuûa baát phöông trình.

– Giaûi baát phöông trình laø tìm taäp nghieäm cuûa baát phöông trình ñoù.

Ví duï 1: Baát phöông trình x > 3 coù taäp nghieäm laø {x | x > 3}. Taäp hôïp naøy ñöôïc bieåu dieãn treân truïc soá nhö hình veõ beân.

Ví duï 2: Baát phöông trình x £ 2 coù taäp nghieäm laø {x | x £ 2}. Taäp hôïp naøy ñöôïc bieåu dieãn treân truïc soá nhö hình veõ beân.

3. Baát phöông trình töông ñöông

Hai baát phöông trình coù cuøng taäp nghieäm laø hai baát phöông trình töông ñöông vaø duøng kí hieäu "Û" ñeå chæ söï töông ñöông ñoù. Ví duï 3: x £ 2 Û 2 ³ x.

II. Baát phöông trình baäc nhaát moät aån

1. Ñònh nghóa

Baát phöông trình daïng ax + b < 0 (hoaëc ax + b > 0, ax + b £ 0, ax + b ³ 0) trong ñoù a vaø b laø hai soá ñaõ cho, a ¹ 0, ñöôïc goïi laø baát phöông trình baäc nhaát moät aån.

2. Hai quy taéc bieán ñoåi baát phöông trình

a) Quy taéc chuyeån veá: Khi chuyeån moät haïng töû cuûa baát phöông trình töø veá naøy sang veá kia ta phaûi ñoåi daáu haïng töû ñoù.

b) Quy taéc nhaân vôùi moät soá: Khi nhaân hai veá cuûa baát phöông trình vôùi cuøng moät soá khaùc 0, ta phaûi:

– Giöõ nguyeân chieàu baát phöông trình neáu soá ñoù döông;

– Ñoåi chieàu baát phöông trình neáu soá ñoù aâm.

3. Caùch giaûi :Baát phöông trình baäc nhaát moät aån ax + b < 0 ñöôïc giaûi nhö sau: ax + b < 0 Û ax < –b (1)

· Neáu a > 0 thì (1) Û x < –                                          · Neáu a < 0 thì (1) Û x > –.

Vaäy nghieäm cuûa baát phöông trình ax + b < 0 laø x < – neáu a > 0; x > – neáu a < 0.

B/ BAØI TAÄP

& BAØI TAÄP CÔ BAÛN

106. Vieát taäp nghieäm cuûa moãi baát phöông trình baèng kí hieäu taäp hôïp, roài bieåu dieãn chuùng treân truïc soá.

a) x < 0                                           b) x > –3.

107. a) AÙp duïng quy taéc nhaân, giaûi caùc baát phöông trình sau :

1. 6x < 18                                  2. –3x > 24                  3. –6x £ –90               4. 8x ³ –40.

b) AÙp duïng quy taéc nhaân, giaûi caùc baát phöông trình sau :

1. x < 4                       2. –x >                           3. x £                 4. –x ³ –.

108. Giaûi thích söï töông ñöông sau :

a) x – 7 < 9 Û x + 3 < 19                          b) –5x ³ 3 Û 20x £ –12.

109. Caùc baát phöông trình sau coù töông ñöông khoâng ? Vì sao ?

a) x – 5 > 0 vaø –2x < –10              b) –2x – 6 < 5 – 3x vaø êx ê < 11.

110. Giaûi caùc baát phöông trình sau vaø bieåu dieãn taäp nghieäm treân truïc soá

a) 3x – 7 > 23                                            c) –2 – 2x £ –10

b) 5x – 9 < 6                                              d) 3 – 10x ³ 33.

111. Cho baát phöông trình (x – 3)² > 0 (1)

a) Chöùng minh raèng : x = 4 ; x = –1 ; x = –3 laø caùc nghieäm cuûa baát phöông trình (1).

b) Coù theå keát luaän raèng vôùi moïi giaù trò cuûa aån soá x ñeàu laø nghieäm cuûa baát phöông trình (1) hay khoâng ?

112. Hình veõ sau bieåu dieãn taäp nghieäm cuûa baát phöông trình naøo ? (Vieát ra hai baát phöông trình coù cuøng taäp nghieäm)

113. Tìm giaù trò cuûa x sao cho :

a) Giaù trò cuûa bieåu thöùc 5x – 8 khoâng aâm.           b) Giaù trò cuûa bieåu thöùc –3x + 5 khoâng döông.

114. Giaûi caùc baát phöông trình vaø bieåu dieãn taäp nghieäm cuûa chuùng treân truïc soá :

a)  < 3                                                       b)  > 5

c)  ³ 7                                                          d)  ³ .

& BAØI TAÄP TRAÉC NGHIEÄM

115. Choïn caâu traû lôøi ñuùng :

Hình veõ naøo döôùi ñaây bieåu dieãn taäp nghieäm cuûa baát phöông trình x £ –2

A. Hình 1                                                                                                                                       B. Hình 2                                                                                                                            C. Hình 3                               D. Hình 4.

& BAØI TAÄP NAÂNG CAO

116. Giaûi caùc baát phöông trình sau :

a)  ³ –3                                b)  < 4

c)  > –19.

117. Giaûi caùc baát phöông trình sau :

a)  >  

b)  £  

c)  < .

118. Giaûi vaø bieän luaän baát phöông trình sau : (m + 2)x > (m + 2)(m – 5).

119. Haõy laäp baát phöông trình cuûa baøi toaùn sau :

Quaõng ñöôøng AB daøi 141 km. Luùc 6 giôø moät moâ toâ khôûi haønh ñi töø A ñeán B, trong giôø thöù nhaát moâ toâ ñi vôùi vaän toác 29 km/giôø. Hoûi trong quaõng ñöôøng coøn laïi moâ toâ phaûi ñi vôùi vaän toác laø bao nhieâu ñeå ñeán B tröôùc 10 giôø 30 phuùt ?

& BAØI THI CHOÏN HOÏC SINH GIOÛI TOAÙN

120. Giaûi caùc baát phöông trình sau :

a) .

(Ñeà thi choïn hoïc sinh gioûi Toaùn lôùp 8, Quaän Taân Bình – TP. Hoà Chí Minh, naêm hoïc 2003 – 2004)

b) x² – 3x > 0.

(Ñeà thi choïn HSG Toaùn 8, Tröôøng  Nguyeãn Du, Quaän 1 – TP. Hoà Chí Minh, naêm hoïc 2000 – 2001)

c)  > 2.

(Ñeà thi choïn HSGToaùn 8, Tröôøng Nguyeãn Gia Thieàu, Quaän Taân Bình – TP.HCM, naêm  2000 – 2001)

§3. PHÖÔNG TRÌNH CHÖÙA DAÁU GIAÙ TRÒ TUYEÄT ÑOÁI

A/ KIEÁN THÖÙC VAØ KÓ NAÊNG CAÀN NHÔÙ

Caùch giaûi phöông trình daïng ½A½ = B

Caùch 1 :                                   ½A½ = B Û 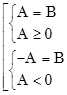                                                                 Caùch 2 :             ½A½ = B Û

· Chuù yù : Neáu vieäc giaûi baát phöông trình trong heä quaù phöùc taïp thì ta chæ caàn giaûi phöông trình trong heä, roài thöû caùc giaù trò vöøa tìm ñöôïc cuûa aån coù thoaû maõn baát phöông trình trong heä hay khoâng. Töø ñoù xaùc ñònh ñöôïc nghieäm cuûa phöông trình ½A½ = B.

B/ BAØI TAÄP

& BAØI TAÄP CÔ BAÛN

121. Boû daáu giaù trò tuyeät ñoái vaø ruùt goïn bieåu thöùc :

a) A = 5x – 9 + ½3x½ trong hai tröôøng hôïp : x ³ 0 vaø x < 0

b) B = x – ½8x½ – 26 trong hai tröôøng hôïp : x £ 0 vaø x > 0

c) C = ½x + 5½ + 6x – 5 khi x ³ –5

d) D = ½13 – x½ + x + 13 khi x > 13.

122. Boû daáu giaù trò tuyeät ñoái vaø ruùt goïn bieåu thöùc :

a) A = 48 + ½2x – 8½ khi x < 4                                   b) B = 6x + ½30 – 6x½ khi x > 5.

123. Boû daáu giaù trò tuyeät ñoái vaø ruùt goïn bieåu thöùc :

a) A = ½x – 7½ + 7                                                                                                                        b) B = ½9 – 3x½ + 3x.

124. Giaûi caùc phöông trình :

a)½x½ – 2x = 15                                                                                                                                        b) ½5x½ + 12 = x.

125. Giaûi caùc phöông trình sau :

a) ½x – 9½ = 2x + 13                                                                                                                     b) ½x + 5½ = 6x – 25.

126. Giaûi caùc phöông trình sau :

a) ½x + 8½ = 4x – 10                                                                                                                     b) ½x – 8½ + 2x = 46.

& BAØI TAÄP TRAÉC NGHIEÄM

127. Choïn caâu traû lôøi ñuùng :

Taäp nghieäm cuûa phöông trình 3½x½ = x + 60 laø :

A. S = {30}                                  B. S = {30; –30}                                                                      C. S = {30; –15}                                                                                                        D. S = {30; 15}.

& BAØI TAÄP NAÂNG CAO

128. Giaûi caùc phöông trình sau :

a) ½x – 1½ – 2½x½ = –2                                                  b) ½x + 1½ + x = ½3x + 2½ + x            c) ½x³ – x – 8½ = x³ + x + 8.

129. Giaûi caùc phöông trình sau :

a) ½2x – 5½ = ½x + 3½                                                                                                                   b) ½x – 1½ = ½3x + 10½.

130. Giaûi caùc phöông trình sau :

a) ½x – 7½ = x – 7                                                                                                                                      b) ½x – 9½ = 9 – x

c) ½x – 1½ = ½1 – x½.

131. Giaûi caùc phöông trình sau :

a) ½x – 5½ + ½x – 2½ = 3                                                                                                              b) ½2x + 5½ + ½2x – 7½ = 12

c) ½5x – 1½ + ½5x + 7½ = 8.

132. Giaûi caùc phöông trình sau :

a) ½x + 5½ + ½x + 7½ + ½x + 15½ = 4x

b) ½x + 1½ + ½x + 2½ + ½x + 3½ + ... + ½x + 2009½ = 2010x.

133. Giaûi caùc phöông trình sau :

a) ½x – 4½²⁰ + ½x – 3½²¹ = 1                            b) ½x – 2009½¹⁹⁶³ + ½x – 2010½¹⁹⁶⁴ = 1.

& BAØI THI CHOÏN HOÏC SINH GIOÛI TOAÙN

134. Giaûi caùc phöông trình sau :

a) ½x² – 5x + 5½ = –2x² + 10x – 11

(Ñeà thi choïn HSG Toaùn 8, Tröôøng  Nguyeãn Du, Quaän 1 – TP. Hoà Chí Minh, naêm hoïc 1998 – 1999)

b) ½2x – 1½ – 3½x + 1½ = 2x + 6

(Ñeà thi choïn hoïc sinh gioûi Toaùn lôùp 8, Quaän 6 – TP. Hoà Chí Minh, naêm hoïc 1999 – 2000)

c) ½x – 1½ + ½x – 5½ = 4

(Ñeà thi choïn HSG Toaùn 8,  Tröôøng  Hoaøng Vaên Thuï, Quaän 10 – TP. HCM, naêm hoïc 2001 – 2002)

135. Giaûi phöông trình :

½2x – ½2x – 1½½ = –m²x  (vôùi m laø tham soá).

(Ñeà thi choïn HSG Toaùn  8, Tröôøng  Hoa Lö, Quaän 9 – TP. Hoà Chí Minh, naêm hoïc 2001 – 2002)