ĐỀ CƯƠNG ÔN TẬP HỌC KÌ II MÔN TOÁN 7
ĐỀ CƯƠNG ÔN TẬP HỌC KÌ II
MÔN TOÁN 7
------------- š&›------------
I.ĐẠI SỐ
A.KIẾN THỨC CƠ BẢN:
1. Số liệu thống kê, tần số.
2. Bảng tần số các giá trị của dấu hiệu
3. Biểu đồ
4. Số trung bình cộng, Mốt của dấu hiệu.
5. Biểu thức đại số.
6. Đơn thức, bậc của đơn thức.
7. Đơn thức đồng dạng, quy tắc công (trừ) đơn thức đồng dạng.
8. Đa thức, cộng trừ đa thức
9. Đa thức một biến, quy tắc cộng (trừ) đa thức một biến
10. Nghiệm của đa thức một biến.
B.CÁC DẠNG BÀI TẬP CƠ BẢN:
Dạng 1: Thu gọn biểu thức đại số:
a) Thu gọn đơn thức, tìm bậc, hệ số của đơn thức.
ŒPhương pháp:
B1: Dùng qui tắc nhân đơn thức để thu gọn.
B2: Xác định hệ số, bậc của đơn thức đã thu gọn.
·Bài tập áp dụng :
1)Thu gọn đơn thức, tìm bậc, hệ số.
2) Tính tích A.B, tìm bậc đơn thức vừa tìm được.
3) Chứng tỏ rằng ba đơn thức  không thể có cùng giá trị âm
không thể có cùng giá trị âm
b) Thu gọn đa thức, tìm bậc, hệ số cao nhất, hệ số tự do của đa thức.
ŒPhương pháp:
B1: nhóm các hạng tử đồng dạng, tính cộng, trừ các hạng tử đồng dạng ( thu gọn đa thức).
B2: bậc của đa thức đã là bậc của hạng tử có bậc cao nhất của đa thức đó.
·Bài tập áp dụng : Thu gọn đa thức, tìm bậc của đa thức.
A=15x2y3 + 7x2 – 8x3y2 – 12x2 + 11x3y2 – 12x2y3
Dạng 2: Tính giá trị biểu thức đại số :
·Phương pháp :
B1: Thu gọn các biểu thức đại số.
B2: Thay giá trị cho trước của biến vào biểu thức đại số.
B3: Tính giá trị biểu thức số.
‚Bài tập áp dụng :
Bài 1 : Tính giá trị biểu thức
d) 2x3 + 5 tại x thỏa mãn x2 – x = 0
Bài 2 : Cho đa thức
a/ P(x) = x4 + 2x2 + 1; b/ Q(x) = x4 + 4x3 + 2x2 – 4x + 1;
Bài 3 : Tính giá trị đa thức
M = x3 + x2y – 2x2 – xy – y2 + 3y + x – 1 với x + y – 2 = 0
Dạng 3 : Cộng, trừ đa thức nhiều biến
ŒPhương pháp :
B1: Viết phép tính cộng, trừ các đa thức.
B2: Áp dụng qui tắc bỏ dấu ngoặc.
B3: Thu gọn các hạng tử đồng dạng ( cộng hay trừ các hạng tử đồng dạng)
·Bài tập áp dụng:
Bài 1 : Cho 2 đa thức :
A = 4x2 – 5xy + 3y2 B = 3x2 + 2xy - y2
Tính A + B; A – B. Tìm đa thức C sao cho C+2B=A
Bài 2 : Tìm đa thức M, N biết :
a/ M + (5x2 – 2xy) = 6x2 + 9xy – y2 b/(3xy – 4y2)- N = x2 – 7xy + 8y2
Dạng 4: Cộng trừ đa thức một biến:
ŒPhương pháp:
B1: Thu gọn các đa thức và sắp xếp theo lũy thừa giảm dần của biến.
B2: Viết các đa thức sao cho các hạng tử đồng dạng thẳng cột với nhau.
B3: Thực hiện phép tính cộng hoặc trừ các hạng tử đồng dạng cùng cột.
Chú ý: A(x) - B(x) = A(x) + [- B(x)]
·Bài tập áp dụng :
Bài 1: Cho đa thức
A(x) = 3x4 – 3/4x3 + 2x2 – 3 B(x) = 8x4 + 1/5x3 – 9x + 2/5
Tính : a/ A(x) + B(x); b/A(x) - B(x); c/ B(x) - A(x);
Bài 2: Cho các đa thức P(x) = x – 2x2 + 3x5 + x4 + x – 1
và Q(x) = 3 – 2x – 2x2 + x4 – 3x5 – x4 + 4x2
a) Thu gọn và sắp xếp các đa thức trên theo lũy thừa giảm của biến.
b) Tính a) M(x) = P(x) + Q(x) b) N(x) = P(x) – Q(x)
c) Tính giá trị M(x) tại x= - 1/2 .
Bài 3: Cho 2 đa thức A(x) = 2x3 - 5x2 + 3x + 3 và B(x) = 2x3 – 4x2 + 3x + 1
a) Tìm đa thức C(x) sao cho C(x) + B(x) = A(x).
b) Tìm nghiệm của đa thức C(x).
Dạng 5 : Tìm nghiệm của đa thức 1 biến
1. Kiểm tra 1 số cho trước có là nghiệm của đa thức một biến hay không?
Phương pháp :
B1: Tính giá trị của đa thức tại giá trị của biến cho trước đó.
B2: Nếu giá trị của đa thức bằng 0 thì giá trị của biến đó là nghiệm của đa thức.
2. Tìm nghiệm của đa thức một biến
Phương pháp :
B1: Cho đa thức bằng 0.
B2: Giải bài toán tìm x.
B3: Giá trị x vừa tìm được là nghiệm của đa thức.
Chú ý :
- Nếu A(x).B(x) = 0 => A(x) = 0 hoặc B(x) = 0
- Nếu đa thức P(x) = ax2 + bx + c có a + b + c = 0
thì ta kết luận đa thức có 1 nghiệm là x1 = 1, nghiệm còn lại x2 = c/a.
- Nếu đa thức P(x) = ax2 + bx + c có a – b + c = 0
thì ta kết luận đa thức có 1 nghiệm là x1 = –1, nghiệm còn lại x2= -c/a.
Bài tập áp dụng :
Bài 1 : Tìm nghiệm của các đa thức sau:
F(x) = (3/4)x – 1/8; H(x) = –5x + 30 G(x) = (x-3)(16-4x)
K(x) = x2-81; M(x) = x2 +7x -8 N(x) = x2 - 2x + 1
A(x) = x3 – x; B(x) = x3 + x C(x) = 5x2 + 10
Bài 2 : Cho 2 đa thức :
A(x) = x + 2x5 + 7x3 – 1 + x2 – 8x – 6x3 – 8
B(x) = -4x2 – x3 +7x – 3 + x4 + 5x3 + 14 – 2x
a) Thu gon và sắp xếp đa thức theo lũy thừa giảm dần của biến.
b) Tính M(x) = A(x) + B(x) ; N(x) = A(x) – B(x)
c) Chứng tỏ x = 2 là nghiệm của N(x) nhưng không phải là nghiệm của M(x)
Bài 3 : Chứng tỏ đa thức : h(x) = x2 + 4 ; f(x) = (x-2)2 + 1 không có nghiệm.
Bài 4 : Cho hai đa thức P(x) = 2x3 + 10x2 – 6x + 7
Q(x) = -2x3 - 8x2 + 6x – 7
a) Tính P(x) + Q(x), P(x) – Q(x).
b) Chứng minh rằng không tồn tại giá trị nào của x để hai đa thức P(x) và Q(x) cùng có giá trị âm.
Bài 5 : Tính nghiệm của đa thức Q(x) = (x-2)2011 – (x – 2)
Dạng 6 : Tìm hệ số chưa biết trong đa thức P(x) biết P(x0) = a
ŒPhương pháp :
B1: Thay giá trị x = x0 vào đa thức.
B2: Cho biểu thức số đó bằng a.
B3: Tính được hệ số chưa biết.
·Bài tập áp dụng :
Bài 1 : Cho đa thức P(x) = mx – 3. Xác định m biết rằng P(–1) = 2
Bài 2 : Cho đa thức Q(x) = -2x2 +mx -7m+3. Xác định m biết rằng Q(x) có nghiệm là -1.
Bài 3 : Xác định hệ số a để đa thức f(x) = ax2 – 4x + 6 có nghiệm là -3
Bài 4 : Cho đa thức P(x) = ax2 + bx + c = 0 .
Chứng tỏ rằng nếu 5a – b + 2c = 0 thì P(-2).P(1) ≤ 0
Dạng 7: Bài toán thống kê.
Bài 1: Thời gian làm bài tập của các học sinh lớp 7 tính bằng phút đươc thống kê bởi bảng sau:
4 5 6 7 6 7 6 4
6 7 6 8 5 6 9 10
5 7 8 8 9 7 8 8
8 10 9 11 8 9 8 9
4 6 7 7 7 8 5 8
a- Dấu hiệu ở đây là gì? Số các giá trị là bao nhiêu?
b- Lập bảng tần số? Tìm mốt của dấu hiệu? Tính số trung bình cộng?
c- Vẽ biểu đồ đoạn thẳng?
Bài 2: Điểm kiểm tra học kỳ môn Toán của các học sinh nữ trong một lớp được ghi lại trong
bảng sau:
5 | 6 | 8 | 7 | 6 | 9 | 8 | 10 | 9 | 7 | 8 | 8 | ||||
7 | 4 | 9 | 5 | 6 | 8 | 9 | 10 |
| |||||||
a) Dấu hiệu ở đây là gì? Lập bảng tần số các giá trị của dấu hiệu.
b) Tính số trung bình cộng và tìm mốt của dấu hiệu.
----------=*=*=*=*=*=*=-----------
II. PHẦN HÌNH HỌC:
A.KIẾN THỨC CƠ BẢN
1. Nêu các trường hợp bằng nhau của hai tam giác, hai tam giác vuông? Vẽ hình, ghi giả
thuyết, kết luận cho từng trường hợp?
2. Nêu định nghĩa, tính chất của tam giác cân, tam giác đều?
3. Nêu định lý Pytago thuận và đảo, vẽ hình, ghi giả thuyết, kết luận của cả hai định lý?
4. Nêu định lý về quan hệ giữa góc và cạnh đối diện trong tam giác, vẽ hình, ghi giả thuyết, kết luận.
5. Nêu quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu, vẽ hình, ghi
giả thuyết, kết luận cho từng mối quan hệ.
6. Nêu định lý về bất đẳng thức trong tam giác, vẽ hình, ghi giả thuyết, kết luận.
7. Nêu tính chất 3 đường trung tuyến trong tam giác, vẽ hình, ghi giả thuyết, kết luận.
8. Nêu tính chất đường phân giác của một góc, tính chất 3 đường phân giác của tam giác, vẽ
hình, ghi giả thuyết, kết luận.
9. Nêu tính chất đường trung trực của một đoạn thẳng, tính chất 3 đường trung trực của tam
giác, vẽ hình, ghi giả thuyết, kết luận.
B. MỘT SỐ PHƯƠNG PHÁP CHỨNG MINH
1. Chứng minh hai đoạn thẳng bằng nhau, hai góc bằng nhau:
C1: Chứng minh hai tam giác bằng nhau.
C2: Sử dụng tính chất bắc cầu, cộng đoạn thẳng, tổng 3 góc, hai góc bù nhau .v. v.
2. Chứng minh tam giác cân:
C1: Chứng minh tam giác đó có hai cạnh bằng nhau hoặc hai góc bằng nhau.
C2: Chứng minh đường trung tuyến đồng thời là đường cao, đường phân giác, đường trung trực của tam giác đó
C3:Chứng minh tam giác có hai đường trung tuyến bằng nhau v.v.
3. Chứng minh tam giác đều:
C1: Chứng minh 3 cạnh bằng nhau hoặc 3 góc bằng nhau.
C2: Chứng minh tam giác cân có 1 góc bằng 600.
4. Chứng minh tam giác vuông:
C1: Chứng minh tam giác có 1 góc vuông.
C2: Dùng định lý Pytago đảo.
C3: Dùng tính chất: "đường trung tuyến ứng với một cạnh bằng nữa cạnh ấy thì tam giác đó là
tam giác vuông"...
5. Chứng minh tia Oz là phân giác của góc xOy:

 C1: Chứng minh xOz = yOz và Oz nằm giữa Ox, Oy .
C1: Chứng minh xOz = yOz và Oz nằm giữa Ox, Oy .
C3: Chứng minh điểm M thuộc tia Oz và cách đều 2 cạnh Ox và Oy.
6. Chứng minh bất đẳng thức đoạn thẳng, góc. Chứng minh 3 điểm thẳng hàng, 3 đường
đồng qui, hai đường thẳng vuông góc v. v. . . (dựa vào các định lý tương ứng).
C. BÀI TẬP ÁP DỤNG
Bài 1 : Cho D ABC cân tại A, đường cao AH. Biết AB=5cm, BC=6cm.
a) Tính độ dài các đoạn thẳng BH, AH?
b) Gọi G là trọng tâm của tam giác ABC. Chứng minh rằng ba điểm A,G,H thẳng hàng?
Bài 2: Cho D ABC cân tại A. Gọi M là trung điểm của cạnh BC.
a) Chứng minh : D ABM = D ACM
b) Từ M vẽ MH ^ AB và MK ^ AC. Chứng minh BH = CK
c) Từ B vẽ BP ^ AC, BP cắt MH tại I. Chứng minh D IBM cân.
Bài 3 : Cho D ABC vuông tại A. Từ một điểm K bất kỳ thuộc cạnh BC vẽ KH ^ AC. Trên tia
đối của tia HK lấy điểm I sao cho HI = HK. Chứng minh :
a) AB // HK
c) BAK = AIK
d) D AIC = D AKC
Bài 4 : Cho D ABC cân tại A ( Â < 90o ), vẽ BD ^ AC và CE ^ AB. Gọi H là giao điểm của
BD và CE.
a) Chứng minh : D ABD = D ACE
b) Chứng minh D AED cân
c) Chứng minh AH là đường trung trực của ED
d) Trên tia đối của tia DB lấy điểm K sao cho DK = DB. Chứng minh ECB = DKC
Bài 5 : Cho D ABC cân tại A. Trên tia đối của tia BA lấy điểm D, trên tia đối của tia CA lấy
điểm E sao cho BD = CE. Vẽ DH và EK cùng vuông góc với đường thẳng BC. Chứng minh :
b) AHB = AKC
c) HK // DE
d) D AHE = D AKD
e) Gọi I là giao điểm của DK và EH. Chứng minh AI ^ DE.
Bài 6: Cho tam giác ABC có B = 900, vẽ trung tuyến AM. Trên tia đối của tia MA lấy điểm E
sao cho ME = MA. Chứng minh:
a) D ABM = D ECM
c) BAM > MAC
d) BE //AC
e) EC ^ BC
Bài 7 : Cho tam giác ABC cân ở A có AB = AC = 5 cm; kẻ AH ^ BC ( H Î BC)
a) Chứng minh BH = HC và BAH = CAH
b) Tính độ dài BH biết AH = 4 cm.
c) Kẻ HD ^ AB ( d Î AB), kẻ EH ^ AC (E Î AC).
d) Tam giác ADE là tam giác gì? Vì sao?
Bài 8 : Cho tam giác ABC vuông tại A (AB < AC), BD là đường phân giác. Vẽ DE^BC tại E
a) Cho biết AB = 6cm , AC = 8cm . Tính BC.
b) Chứng minh tam giác DAE cân.
c) Chứng minh rằng DA < DC.
d) Vẽ CF vuông góc với BD tại F. Chứng minh rằng các đường thẳng AB, DE, CF đồng quy.
Bài 9 : Cho tam giác ABC cân tại A , AD là đường phân giác. Trên tia đối của tia DA lấy điểm E sao cho DE = DA.
a) Chứng minh rằng D là trung điểm cạnh BC.
b) Chứng minh rằng tam giác BAE cân.
c) Gọi M là trung điểm cạnh AC, N là giao điểm của BC và EM.
Chứng minh rằng BC = 3NC
Bài 10 : Cho tam giác ABC vuông tại A(AB < AC), BE là đường phân giác. Trên cạnh BC lấy điểm D sao cho BD = BA.
a) Chứng minh : D ABD cân và BE ^ AD.
b) Chứng minh tam giác EAD cân.
c) Trên tia đối của tia AB lấy điểm F sao cho AF = DC. Chứng minh rằng D EFC cân.
d) Chứng minh : D, E, F thẳng hàng.
Bài 11 : Cho tam giác ABC có AM là đường trung tuyến. Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
a) Chứng minh rằng AB = CD, AB // CD.
c) Trên đoạn thẳng AM lấy K sao cho AK = 2MK. Gọi N lả giao của CK và AB. Chứng minh rằng AN = BN.
Bài 12 : Cho tam giác ABC cân tại A, AM là đường trung tuyến.
a) Cho biết AB = AC = 13cm, BC = 10cm. Tính AM.
b) Vẽ AN là đường trung tuyến của tam giác ABM. Gọi D là điểm sao cho N là trung điểm đoạn thẳng AD, E là trung điểm đoạn thẳng CD. Chứng minh rằng A, M, E thẳng hàng.
Bài 13 : Cho ∆ ABC có góc A = 90° . Đường trung trực của AB cắt AB tại E và BC tại F
a/ Chứng minh FA = FB
b/ Từ F vẽ FH ^ AC ( HÎAC ) Chứng minh FH ^ EF
c/ Chứng minh FH = AE
d/ Chứng minh EH = BC/2; EH // BC
Bài 14: Cho tam giác ABC (AB < AC) có AM là phân giác của góc A.(M thuộc BC).Trên AC
lấy D sao cho AD = AB.
a. Chứng minh: BM = MD
b. Gọi K là giao điểm của AB và DM .Chứng minh: DDAK = DBAC
c. Chứng minh : DAKC cân
d. So sánh : BM và CM.
Bài 15 : Cho ∆ ABC cân tại A. Trên tia đối của tia BC lấy M, trên tia đối của tia CB lấy N sao cho BM = CN. Vẽ BD ^ AM tại D, CE ^ AN tại E.
a) Chứng minh rằng tam giác AMN cân.
b) Chứng minh rằng BD = CE.
c) Gọi K là giao điểm của DB và EC. Chứng minh rằng ∆ADK = ∆AEK.
d) Chứng minh rằng KD + KE < 2KA
Bµi 16: Cho tam gi¸c ABC cã AB < AC, ph©n gi¸c AM. Trªn tia AC lÊy ®iÓm N sao cho AN = AB. Gäi K lµ giao ®iÓm cña c¸c ®êng th¼ng AB vµ MN. Chøng minh r»ng:
a) MB = MN b)D MBK = D MNC c) AM ^ KC vµ BN // KC d) AC – AB > MC – MB
Bµi 17: Cho tam gi¸c ABC vu«ng t¹i A. VÏ ®êng cao AH. Trªn c¹nh BC lÊy ®iÓm D sao cho BD = BA.
a) 
 Chøng minh r»ng: tia AD lµ tia ph©n gi¸c cña HAC
Chøng minh r»ng: tia AD lµ tia ph©n gi¸c cña HAC
b) VÏ DK ^ AC (K Î AC). Chøng minh r»ng: AK = AH.
c) Chøng minh r»ng: AB + AC < BC + AH.
Bµi 18: Cho D ABC c©n t¹i A. KÎ ph©n gi¸c AD ( D Î BC ). Trªn tia ®èi cña tia AB lÊy ®iÓm E sao cho
AE = AB. Trªn tia ph©n gi¸c cña CAE lÊy ®iÓm F sao cho AF = BD. Chøng minh r»ng:
a. AD ^ BC b. AF // BC c. EF = AD d. C¸c ®iÓm E, F, C th¼ng hµng.
Bµi 19: Cho tam gi¸c ABC. Gäi E, F theo thø tù lµ trung ®iÓm cña c¸c c¹nh AB, AC. Trªn tia ®èi cña tia FB lÊy ®iÓm P sao cho PF = BF. Trªn tia ®èi cña tia EC lÊy ®iÓm Q sao cho QE = CE.
a) Chøng minh: AP = AQ
b) Chøng minh ba ®iÓm P, A, Q th¼ng hµng.
c) Chøng minh BQ // AC vµ CP // AC
d) Gäi R lµ giao ®iÓm cña hai ®êng th¼ng PC vµ QB. Chøng minh r»ng chu vi  PQR b»ng hai lÇn chu vi
PQR b»ng hai lÇn chu vi  ABC.
ABC.
e)  Ba ®êng th¼ng AR, BP, CQ ®ång quy.
Ba ®êng th¼ng AR, BP, CQ ®ång quy.

 Bµi 20: Cho D ABC c©n t¹i A cã BC < AB. §êng trung trùc cña AC c¾t ®êng th¼ng BC t¹i M. Trªn tia ®èi cña tia AM lÊy ®iÓm N sao cho AN = BM.
Bµi 20: Cho D ABC c©n t¹i A cã BC < AB. §êng trung trùc cña AC c¾t ®êng th¼ng BC t¹i M. Trªn tia ®èi cña tia AM lÊy ®iÓm N sao cho AN = BM.
a) Chøng minh r»ng: AMC=BAC b). Chøng minh r»ng: CM = CN
c) Muèn cho CM ^ CN th× tam gi¸c c©n ABC cho tríc ph¶i cã thªm ®iÒu kiÖn g×?
Bµi 21: Cho D ABC vµ mét ®iÓm O n»m trong tam gi¸c. Chøng minh r»ng:
Tags: THCS Nguyễn Du, Toán Lớp 7, Toán THCS

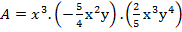











 Trang Trước
Trang Trước





No comments: