Bài

Giải tóm tắt

Điểm

B1

(3.5đ)

B2

1.(1.đ) Tìm khoảng đơn điệu và CTcủa các h/s: 1)   

+ TXĐ :D=R  ------------------------------------------------------------------------------

+ --------------------------------------------

+BBT: x                            -3                        1                          

                               _           0           +             0           +                                                                        

            y                                                                                      

ĐB:     ;   CT --------------------------------------

2)(1.5đ )           +TXĐ : D=--------------------------------------

+ --------------------------------------------------

+BBT:  x                -2                                             2

                                        -         0           +        0         -            

              y                 0                                          2  

                                                       -2                                    0        

ĐB:;CĐ

3)(1.0đ)            với

------------------------------------------------------

+ n là số nguyên lẽ thì :n-1 chẵn

   y^/ theo dấu của :Lập bảng BT ta có kq:

   NB :;ĐB:------------------------------------------

   CĐ:;CT:-------------------------------------------

+ n nguyên chẵn thì n-1 lẽ nên cùng dấu với x lập bảng BT ta có kq

ĐB :;NB:

1) (1.0đ)         Tìm giá trị lớn nhất ,giá trị nhỏ nhất của hàm số:

                                  với

+---------------------------------------------------------------

-----------------------------------

     --------------------------------

0.25

0.25

0.25

0.25

0.25

0.25+

0.25

0.25

0.25+

0.25

0.25

0.25

0.25

0.25

0.25

0.25+

0.25

0.25

B2

2)(1.0đ)  Hàm số  (C) Chứng tỏ rằng các tiếp tuyến với ( C) đi qua điểm M(2;-1) thì vuông góc với nhau .

+Tiếp tuyến với ( C) tại có PT:

( d); do (d) đi qua M(2;-1)--------------

---------------------------------------------------------------------------

Có 2 tiếp tuyến qua M(2;-1) với:

Hoặc 2TT là :( T₁) :( T₂)

Từ đó xét tích 2 hệ số góc bằng -1 có (đpcm)

0.25+

0.25

0.25

0.25

B3

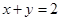(1.0đ)   Cho  và x,y .   Chứng minh rằng :   ( 1)

Từ gt : ----------------------------

Xét hàm --------------------------

-------------------------------------------------------------------

BBT : x                               1                           

                          -            0            +

                                                   2

Từ BBT (đpcm)

0.25

0.25

0.25

0.25

B4

3.5đ

Hình vẽ :

1)Chứng minh SC(AHK)        (1.0đ)

CDAD (gt)

CDSA (vì SA(ABCD))CD(SAD) CDAK (1 )----------------------

SDAK (2 ) từ  (1 )& (2) AK(SCD)AKSC (* )-------------------------

Tương tự chứng minh được AHSC ( **)---------------------------------------------

Từ (*) & (** )  SC(AHK) (đpcm)-------------------------------------------------

2)Tính góc giữa 2 mặt phẳng (SCB) và (SCD)  (1.0đ)

+Nêu được :------------------------

+Chỉ ra được :------------------------------------------------

+ góc :------------------------------------------------------------------

3)Tính khoảng cách giữa :AC và SD.(1.0đ)

Dựng Dt // AC ta có AC // (S;Dt )

d (AC,SD )=d(A,(S,Dt)-------------------------------------------------------------------

Dựng AI Dt (1 ) Vì Dt// AC nên Dt(ABCD) DtSA (2)

 Từ (1) & (2)  Dt ( SAI)

Dựng AESI AEDt -----------------

Tứ giác AIDO là hình vuông nên -----------------------------------

-----------------------------------------------

Vậy :

0.5

0.25

0.25

0.25

0.25

0.25+

0.25

0.25

0.25

0.25

0.25

0.25

0.25