ĐỀ THI HỌC KỲ II MÔN TOÁN KHỐI 12
Sở giáo dục và đào tạo Kiên Giang
Trường THPT chuyên Huỳnh Mẫn Đạt
ĐỀ THI HỌC KỲ II MÔN TOÁN KHỐI 12
NĂM HỌC 2010-2011
Thời gian làm bài : 150 phút (không kể thời gian phát đề)
A. PHẦN CHUNG (6.0Đ)
Bài 1.(3.0 điểm) Tính các tích phân sau
a/ 
b/
c/
d/ 
Bài 2.(1.0 điểm) Tính diện tích hình phẳng giới hạn bởi :
.
Bài 3.(2.0 điểm)
a. Cho hai số phức 
và 
. Tính z1.z2.
b. Tìm số phức z thỏa mãn : 
.
B. PHẦN RIÊNG (4.0Đ)
1. Theo chương trình chuẩn (Dành cho lớp Văn-A5):
Bài 4a. (1.0 điểm) Giải phương trình sau trên tập số phức
3z2 – 5z + 10 = 0
Bài 5a. (2.0 điểm) Trong không gian Oxyz, cho 
với 
lần lượt là các vec tơ đơn vị của trục x'Ox, y'Oy và z'Oz.
a. Viết phương trình mặt phẳng 
qua ba điểm là hình chiếu vuông góc của A lên các trục tọa độ.
b. Tìm hình chiếu vuông góc của gốc tọa độ O lên mặt phẳng .
c. Viết phương trình mặt cầu (S) có tâm là B và tiếp xúc với mặt phẳng (P) chứa Oz và song song AB.
Bài 6a. (1 điểm) Trong không gian Oxyz, đường thẳng 
và các điểm
, 
, 
.Tìm tọa độ điểm M trên d sao cho
nhỏ nhất.
2. Theo chương trình nâng cao (Các lớp còn lại):
Bài 4b. (1.0 điểm) Giải phương trình sau trên tập số phức
z2 – 2(2 + i)z + 7 + 4i = 0.
Bài 5b: (2.0 điểm)
Trong không gian Oxyz, cho tam giác ABC, A(1;1;0), B(0;2;1), trọng tâm G của tam giác
ABC là G(0;2;-1).
a. Tính khoảng cách từ A đến đường thẳng BC.
b. Tìm tọa độ trực tâm H của tam giác ABC.
c. Tìm tọa độ điểm M thuộc đường thẳng (d), biết (d) đi qua G và (d) vuông góc mặt phẳng
(ABC) sao cho thể tích tứ diện MABC bằng 
(đvtt).
Bài 6b: (1.0điểm)
Trong không gian Oxyz, cho đường thẳng (d) :
Viết phương trình mặt phẳng (P) chứa đường thẳng (d) tạo với Oy góc lớn nhất.
--HẾT--
Họ và tên thí sinh:………………………………… SBD:……………….
ĐÁP ÁN TOÁN HỌC KÌ II
Bài | Đáp án | Điểm |
1 | 3.0 | |
1.a (0,75đ) |
| 0,25 |
| 0,25 | |
| 0,25 | |
1.b (0,75đ) |
Đặt | 0,25 |
| 0,25 | |
| 0,25 | |
1.c (0,75đ) |
Đặt | 0,25 |
| 0,25 | |
| 0,25 | |
1.d (0,75đ) |
Đặt
| 0,25 |
Đặt
| 0,25 | |
| 0,25 | |
2 | 1.0 | |
Phương trình hoành độ giao điểm giữa
| 0,25 | |
Diện tích hình phẳng S được tính bởi
| ||
Đặt | 0,25 | |
| ||
| 0,25 | |
| 0,25 | |
3 | 2.0 | |
3.a (1,0 đ) | Ta có | 0,25 |
| 0,25 | |
Suy ra | 0,5 | |
3.b (1,0 đ) | Ta có
| 0,25 |
| 0,25 | |
| 0,5 | |
Chương trình nâng cao | ||
4b | 1.0 | |
Ta có: | 0,5 | |
Phương trình có 2 nghiệm phân biệt là: | 0,5 | |
5b | 2.0 | |
a. (0,75 đ) | Gọi Do G là trọng tâm tam giác ABC, ta có
| 0,25 |
| 0,25 | |
| ||
Khoảng cách từ A đến đường thẳng BC
| 0,25 | |
b. (0,5 đ) | Gọi
| 0,25 |
Từ giả thiết ta có hệ sau:
| ||
| 0,25 | |
c. (0,75 đ) | Đường thẳng (d) vuông góc (ABC) nên có vec tơ chỉ phương | 0,25 |
| ||
| 0,25 | |
| ||
| 0,25 | |
Có hai điểm thỏa mãn đề là | ||
6b | 1.0 | |
Đường thẳng (d) qua | 0,25 | |
(P) chứa (d) nên qua
| ||
Ta có | ||
Gọi
| 0,25 | |
Từ (2) suy ra | ||
· Nếu B = 0 thì | 0,25 | |
· Nếu
| ||
Cả hai trường hợp Vậy (P) cần tìm có phương trình : | 0,25 | |
Chương trình chuẩn | ||
4a | 1.0 | |
Ta có | 0,5 | |
Vậy phương trình có hai nghiệm: | 0,5 | |
5a | 2.0 | |
a. (0,5 đ) | Ta có:
| 0,25 |
Phương trình mặt phẳng | 0,25 | |
b. (0,75 đ) | Gọi (d) là đường thẳng qua O và vuông góc với mặt phẳng | 0,25 |
H là hình chiếu của O lên mặt phẳng | 0,25 | |
| ||
Vậy | 0,25 | |
c. (0,75 đ) | Ta có Viết được mặt phẳng (P): | 0,25 |
Bán kính mặt cầu (S)
| 0,25 + 0,25 | |
6a | 1.0 | |
| 0,25 | |
| 0,25 | |
Đẳng thức xảy ra khi | 0,25 | |
Vậy | 0,25 |
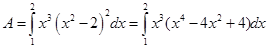
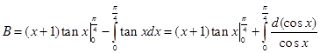
Trang Trước
No comments: